DAY 5模拟赛

DAY 5

廖俊豪神仙出题

---

T1

最小差异矩阵（a.cpp, a.in, a.out）

【题目描述】

有一个 n*m 的矩阵，矩阵的每个位置上可以放置一个数。对于第 i 行，第 i 行的差异定义为该行的最大数和最小数的差。一个矩阵的差异，定义为矩阵中每一行差异的最大值。现在给定 k 个数 v[1..k]，问：从这 k 个数中选 n*m 个数放入矩阵，能够得到的矩阵的差异最小值是多少。

【输入格式】

第一行三个整数，k, n, m，表示有 k 个数可选，矩阵的行数和列数分别为 n 和 m。

第二行 k 个整数，表示备选的数 v[1..k]。

【输出格式】

输出一个数，表示能够得到的最小差异值

【样例输入】

5 2 2

7 5 8 2 3

【样例输出】

1

【数据范围与提示】

对于 30%的数据，k <= 10, n <= 3, m <= 3

对于 100%的数据，n * m <= k <= 100000, n, m <= 1000，0 <= v[i] <= 10^9

256MB，1s

题解

先排序

二分差异的最大值k,然后贪心

放数一定是连续的,将某一段放到一行

从前往后找,如果说从某个数开始往后数m个数,最大值减去最小值小于等于枚举的k就合法,那么就把这m个数放到同一行,最后判断是否能够凑出n行

O(klogC)

#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e5 + ;
int n, m, k, v[maxn];

int judge(int d)
{
    int tmp = ;
    for (int i=; i+m-<=k; ++i)
    {
        if (v[i+m-] - v[i] <=d)
            ++tmp, i += m - ;
    }
    if (tmp >= n) return ;
    return ;
}

int main()
{
    freopen("a.in", "r", stdin);
    freopen("a.out", "w", stdout);
    scanf("%d%d%d", &k, &n, &m);
    for (int i=; i<=k; ++i)
        scanf("%d", &v[i]);
    sort(v + , v + k + );
    int left = , right = 1e9;
    while (left < right)
    {
        int mid = (left + right) / ;
        if (judge(mid))
            right = mid;
        else
            left = mid + ;
    }
    printf("%d\n", left);
    return ;
}

---

T2

分割序列（b.cpp, b.in, b.out）

【题目描述】

给定一个长度为 n 的序列 v[1..n]，现在要将这个序列分成 k 段（每段都不能为空），定义每一段的权值为该段上的所有数的或和。定义整个序列的权值为每段权值的和。问：这个序列的最大权值为多少。

【输入格式】

第一行两个数 n 和 k，意义如题意所示。

第二行 n 个数，表示这个序列 v[1..n]。

【输出格式】

输出一个数，代表这个序列的最大权值。

【输入样例】

5 2

7 5 8 2 3

【输出样例】

22

【数据范围与时空限制】

对于 30%的数据，n <= 10, k <= 10

对于 60%的数据，n <= 100, k <= 100

对于 100%的数据，k <= n <= 2000，1 <= v[i] <= 5 * 10^5

256MB，1s

题解

f[i][j]表示前i个数分j段的最大权值和  ans=f[n][k]

可以先预处理出每一段的或和sum[i][j]

转移：f[i][j]=max(f[l][j-1]+sum[l+1][i])(l<i) l表示将第i+1到第i个数当成一段

60pts

怎么优化？

还是先n^2预处理

找单调性  f[l][j-1]随着l的增加递增  sum[l+1][i]随着l的增加而递减

Sum是按位或：比如变化到1e6，最多变化20次

如果按sum值分段，那么最优的一定是某一段sum的最后加上f的值

那么对于每一个j，我们可以枚举它前面的点i，把sum分段

If(sum[i][j]!=sum[i+1][j])  vector[j].push_back(i);

在刚才枚举l的时候就可以变成枚举决策点了，这一维变成了log的复杂度

O(n*k*logC)

#include <bits/stdc++.h>
using namespace std;

const long long inf = 1ull <<  << ;
const int maxn = ;
vector<int> point[maxn];
int n, K, v[maxn], sum[maxn][maxn];
long long f[maxn][maxn];
int main()
{
    freopen("b.in", "r", stdin);
    freopen("b.out", "w", stdout);
    cin >> n >> K;
    for (int i=; i<=n; ++i) cin >> v[i];
    for (int i=; i<=n; ++i) sum[i][i] = v[i];
    for (int i=; i<n; ++i)
        for (int j=i+; j<=n; ++j)
            sum[i][j] = sum[i][j-] | v[j];
    for (int i=; i<=n; ++i)
    {
        point[i].push_back(i);
        for (int j=i-; j>=; --j)
            if (sum[j][i] != sum[j+][i])
                point[i].push_back(j);
    }
    for (int k=; k<=K; ++k)
        for (int i=; i<=n; ++i)
        {
            if (i < k) continue;
            for (int j=; j<point[i].size(); ++j)
            {
                int x = point[i][j];
                if (x >= k)
                    f[i][k] = max(f[i][k], f[x-][k-] + sum[x][i]);
            }
        }
    cout << f[n][K] << endl;
    return ;
}

---

T3

树的魔法值（C.cpp, C.in, C.out）

【题目描述】

有一棵 k+1 层的满二叉树，那么该树有 2^k 个叶子节点。给定 n 个机器人(n=2^k)，编号从 1—n，编号为 i 的机器人的权值为 v[i]。我们现在要将这 n 个机器人分别放置在这 n 个叶子节点上，每个叶子节点放且只能放一个机器人。叶子节点的权值为该叶子节点上的机器人的权值。非叶子节点的权值定义为该树中编号最大的机器人的权值。每个非叶子节点除了权值以外，还有一个魔法值，该点的魔法值为其左右儿子节点的权值的乘积。整棵树的魔法值定义为非叶子节点的魔法值的和。

问：将这 n 个机器人随机地放在这 n 个叶子节点上，树的魔法值的期望为多少。

【输入格式】

第一行为一个整数 k，含义如题所示。

第二行为 2^k 个整数，依次表示这 n 个机器人的权值。

【输出格式】

假设答案为一个不可约分数 P/Q，则输出在模 1e9+7 意义下的 P * (Q^-1)模 1e9+7 的值。

【样例输入 1】

2

1 3 5 7

【样例输出 1】

59

【样例解释】

对于 n=4 的情况，机器人共有 24 种不同的安放方案。其中，本质不同的有 3 种，分别是((1,3),(5,7)), ((1,5),(3,7)), ((1,7),(5,3))，魔法值分别为 1*3+5*7+3*7=59, 1*5+3*7+5*7=61,1*7+5*3+5*7=57, 答案为（57+59+61）/3 = 59。

【样例输入 2】

2

1 5 3 7

【样例输出 2】

333333390

【数据范围与时空限制】

30%的数据，k <= 3

60%的数据，k <= 10

100%的数据，k <= 18

256MB，1s

题解：

30pts  k<=3 --> n<=8  n!暴力  期望：所有情况的值加起来取平均  就是除以n！

60pts  k<=10,n<=1024  求出所有情况的魔法值的和？

考虑两个点x和y在第d层对答案的贡献

分步考虑  考虑两个点在第d层相遇，那么应该算清楚第d层相遇了多少次，统计出来就可以算出贡献

Σ(v[x]*v[y]*times[x][y])

怎么算？

设x>y

在y的子树里面，一定有2^d-1个小于y的

1）在y-1个数里面，选择2^d -1个小于y的方案数C(y -1, 2^y -1)

2）在x- 2^d -1个数里面，选择2^d -1个小于x的方案数 C(x- 2^d -1 , 2^d-1)

3) 其他n- 2^(d+1) 任意排列n- 2^(d+1)！

4) 考虑x和y相遇的位置  2^(k-d)

5) 上面的都不对，因为要求排列，所以是A

6) x和y的位置可以互换  *2

x>2^(d+1)  y>=2^d  x>y

bits[i]表示2^i

c[i][j]表示C(i,j)

fac[i]表示i!

枚举x，y，d

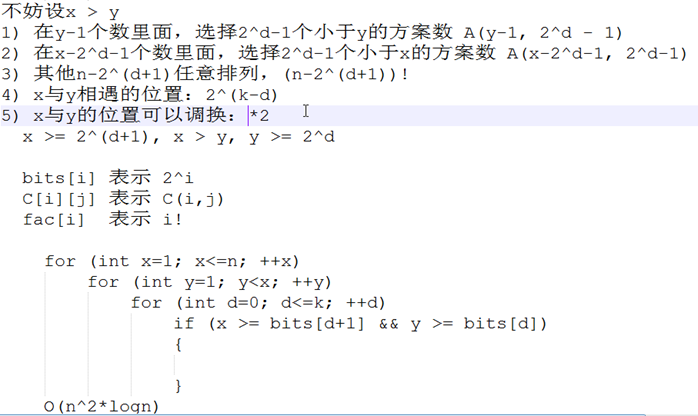
O(n^2logn)

100pts

优化式子本身

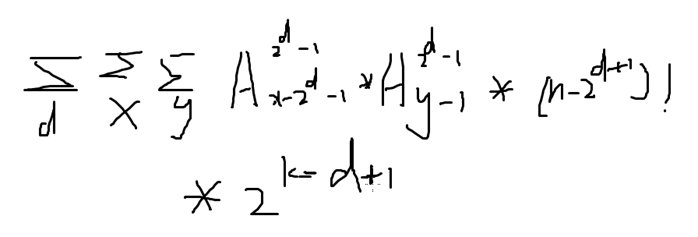
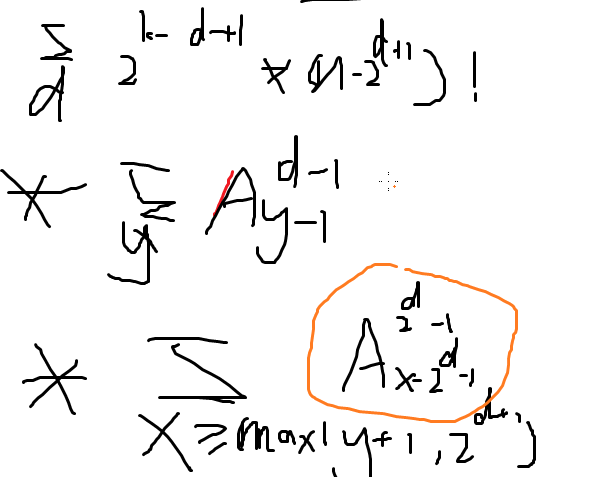
发现最后一部分只在枚举x的时候和y有关，所以可以把它放到外面去

预处理出后缀和，枚举d和y就行了

#include <bits/stdc++.h>
using namespace std;

const int mod = 1e9 + ;
const int maxn = ( << ) + ;
typedef long long LL;

LL fac[maxn], inv_fac[maxn], bit[maxn], sum[maxn];
int n, v[maxn], k;
int powmod(int x, int times)
{
    LL tmp = ;
    while (times > )
    {
        if (times & ) tmp = tmp * x % mod;
        x = (LL)x * x % mod;
        times >>= ;
    }
    return tmp;
}

LL C(int x, int y)
{
    if (x < y) return ;
    return fac[x] * inv_fac[y] % mod * inv_fac[x-y] % mod;
}

int main()
{
    freopen("c.in", "r", stdin);
    freopen("c.out", "w", stdout);
    fac[] = ; for (int i=; i<maxn; ++i) fac[i] = fac[i-] * i % mod;
    inv_fac[maxn-] = powmod(fac[maxn-], mod - );
    for (int i=maxn-; i>=; --i) inv_fac[i] = inv_fac[i+] * (i + ) % mod;
    bit[] = ; for (int i=; i<=; ++i) bit[i] = bit[i-] * ;

    scanf("%d", &k);
    n = bit[k];
    for (int i=; i<=bit[k]; ++i) scanf("%d", &v[i]);
    //for (int i=bit[k]; i>=1; --i) scanf("%d", &v[i]);
    LL ans = ;
    for (int d=; d<=k; ++d)
    {
        LL tmp = ;
        for (int i=n; i>=bit[d]; --i)
            sum[i] = (sum[i+] + C(i--bit[d-], bit[d-]-) * v[i]) % mod;
        for (int j=n-; j>=bit[d-]; --j)
            tmp = (tmp + C(j-, bit[d-]-) * v[j] % mod * sum[max(bit[d], (LL)j + )]) % mod;
        ans = (ans + tmp * fac[bit[d-]] % mod * fac[bit[d-]] % mod * fac[n-bit[d]] % mod
                *  % mod * bit[k-d]) % mod;
    }
    ans = ans * inv_fac[n] % mod;
    cout << ans << endl;
    return ;
}