[BZOJ 4771]七彩树(可持久化线段树+树上差分)

[BZOJ 4771]七彩树(可持久化线段树+树上差分)

题面

给定一棵n个点的有根树，编号依次为1到n，其中1号点是根节点。每个节点都被染上了某一种颜色，其中第i个节点的颜色为c[i]。如果c[i]=c[j]，那么我们认为点i和点j拥有相同的颜色。定义depth[i]为i节点与根节点的距离。为了方便起见，你可以认为树上相邻的两个点之间的距离为1。站在这棵色彩斑斓的树前面，你将面临m个问题。

每个问题包含两个整数x和d，表示询问x子树里且depth不超过depth[x]+d的所有点中出现了多少种本质不同的颜色。请写一个程序，快速回答这些询问。

分析

先不考虑深度限制，我们考虑如何统计颜色。

我们把每种颜色开一个set，set里存储该颜色节点的dfs序。对于一对相同颜色的节点u,v，他们会对u到v的路径上的节点，和lca(u,v)到根节点路径上的节点的答案产生1的贡献。可以用树上差分算法。开一棵线段树，线段树第x个叶子节点存储节点dfs序（记作dfn) 为x的差分值，维护区间和。那么我们把dfn[u]+1,dfn[v]+1,dfn[lca(u,v)]-1即可。查询x子树的时候直接区间查询x的dfs序对应的区间。

那么我们加入一个新节点x的时候如何更新答案呢。这实际上是在处理树链的并。我们在set中找出x的前驱pre和后继nex（按照dfn排序后），dfn[x]+1,dfn[lca(pre,x)]-1,相当于把x到lca(pre,x)的路径加入答案。同理对nex进行操作。注意lca(pre,nex)往上的路径被减了两次，所以dfn[lca(pre,nex)] -1.这里画个图可以方便理解

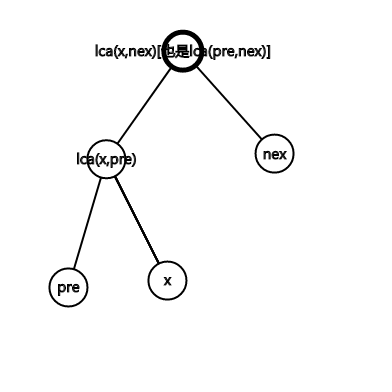
那么有深度限制要怎么做呢？维护可持久化线段树，第i棵可持久化线段树存储深度<=i的树的答案，把节点按深度排序。依次加入对应深度的可持久化线段树。查询的时候直接在对应的线段树中查询x子树即可。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<set>
#define maxn 400000
#define maxlogn 32
using namespace std;
inline int qread(int &x){
	x=0;
	int sign=1;
	char c=getchar();
	while(c<'0'||c>'9'){
		if(c=='-') sign=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9'){
		x=x*10+c-'0';
		c=getchar();
	}
	return x*sign;
}
inline void qprint(int x){
	if(x<0){
		putchar('-');
		qprint(-x);
	}else if(x==0){
		putchar('0');
		return;
	}else{
		if(x/10>0) qprint(x/10);
		putchar('0'+x%10);
	}
}
int t,n,m;
int c[maxn+5];
struct edge{
	int from;
	int to;
	int next;
}E[maxn*2+5];
int sz=1;
int head[maxn+5];
void add_edge(int u,int v){
	sz++;
	E[sz].from=u;
	E[sz].to=v;
	E[sz].next=head[u];
	head[u]=sz;
}

int log2n;
int tim;
int anc[maxn+5][maxlogn+5];
int hash_dfn[maxn+5];
int deep[maxn+5];
int lb[maxn+5],rb[maxn+5];
int id[maxn+5];
int cmp(int x,int y){
	return deep[x]<deep[y];
}

void dfs(int x,int fa){
	tim++;
	lb[x]=tim;
	deep[x]=deep[fa]+1;
	anc[x][0]=fa;
	hash_dfn[lb[x]]=x;
	for(int i=1;i<=log2n;i++) anc[x][i]=anc[anc[x][i-1]][i-1];
	for(int i=head[x];i;i=E[i].next){
		int y=E[i].to;
		if(y!=fa){
			dfs(y,x);
		}
	}
	rb[x]=tim;
}

int lca(int x,int y){
	if(deep[x]<deep[y]) swap(x,y);
	for(int i=log2n;i>=0;i--){
		if(deep[anc[x][i]]>=deep[y]){
			x=anc[x][i];
		}
	}
	if(x==y) return x;
	for(int i=log2n;i>=0;i--){
		if(anc[x][i]!=anc[y][i]){
			x=anc[x][i];
			y=anc[y][i];
		}
	}
	return anc[x][0];
}
struct per_segment_tree{
	//第i棵可持久化线段树维护deep<=i,且dfn在[l,r]内的节点的不同颜色个数
	struct node{
		int ls;
		int rs;
		int cnt;
	}tree[maxn*maxlogn+5];
	int root[maxn+5];
	int ptr;
	void push_up(int x){
		tree[x].cnt=tree[tree[x].ls].cnt+tree[tree[x].rs].cnt;
	}
	void insert(int &x,int last,int upos,int uval,int l,int r){
		x=++ptr;
		tree[x]=tree[last];
		if(l==r){
			tree[x].cnt+=uval;
			return;
		}
		int mid=(l+r)>>1;
		if(upos<=mid) insert(tree[x].ls,tree[last].ls,upos,uval,l,mid);
		else insert(tree[x].rs,tree[last].rs,upos,uval,mid+1,r);
		push_up(x);
	}
	int query(int x,int L,int R,int l,int r){
		if(x==0) return tree[x].cnt;
		if(L<=l&&R>=r){
			return tree[x].cnt;
		}
		int mid=(l+r)>>1;
		int ans=0;
		if(L<=mid) ans+=query(tree[x].ls,L,R,l,mid);
		if(R>mid) ans+=query(tree[x].rs,L,R,mid+1,r);
		return ans;
	}
}T;

set<int>s[maxn+5];
void ini(){
	log2n=log2(n)+1;
	tim=0;
	sz=1;
	T.ptr=0;
	for(int i=1;i<=n;i++){//不要memset,会TLE
		anc[i][0]=0;
		c[i]=0;
		deep[i]=0;
		hash_dfn[i]=0;
		head[i]=0;
		id[i]=0;
		lb[i]=0;
		rb[i]=0;
		s[i].clear();
		T.root[i]=0;
	}
}
int main(){

	int u,v;
	qread(t);
	while(t--){

		qread(n);
		qread(m);
		ini();

		for(int i=1;i<=n;i++) qread(c[i]);
		for(int i=2;i<=n;i++){
			qread(u);
			add_edge(u,i);
			add_edge(i,u);
		}
		dfs(1,0);
		for(int i=1;i<=n;i++) id[i]=i;
		sort(id+1,id+1+n,cmp);
		for(int i=1;i<=n;i++){
			int x=id[i];
			int pre=0,nex=0;

			T.insert(T.root[deep[x]],T.root[deep[id[i-1]]],lb[x],1,1,n);
			set<int>::iterator it=s[c[x]].lower_bound(lb[x]);
			if(it!=s[c[x]].begin()){
				set<int>::iterator it2=it;//不能直接--it,会影响下一个判断
				pre=hash_dfn[*(--it2)];

				T.insert(T.root[deep[x]],T.root[deep[x]],lb[lca(pre,x)],-1,1,n);
				//x会对pre到x的路径上的点产生1的贡献，树上差分
				//线段树里的每个店储存的都是差分值
			}
			if(it!=s[c[x]].end()){
				nex=hash_dfn[*it];

				T.insert(T.root[deep[x]],T.root[deep[x]],lb[lca(x,nex)],-1,1,n);
			}
			//lca(pre,nex)上方的路径被多减了一次，加回来
			if(pre!=0&&nex!=0){

				T.insert(T.root[deep[x]],T.root[deep[x]],lb[lca(pre,nex)],1,1,n);
			}
			s[c[x]].insert(lb[x]);
		}

		int last=0;
		int x,d;
		for(int i=1;i<=m;i++){
			qread(x);
			qread(d);
			x^=last;
			d^=last;
			last=T.query(T.root[min(deep[x]+d,deep[id[n]])],lb[x],rb[x],1,n);
			qprint(last);
			putchar('\n');
		}
	}
}