gcc数据结构对齐之：why.

　　gcc 支持 aligned 和 packed 属性指定数据对齐，那么在了解对齐规则之前，需要解决第一个以为，我们为什么需要数据对齐？请看下图：

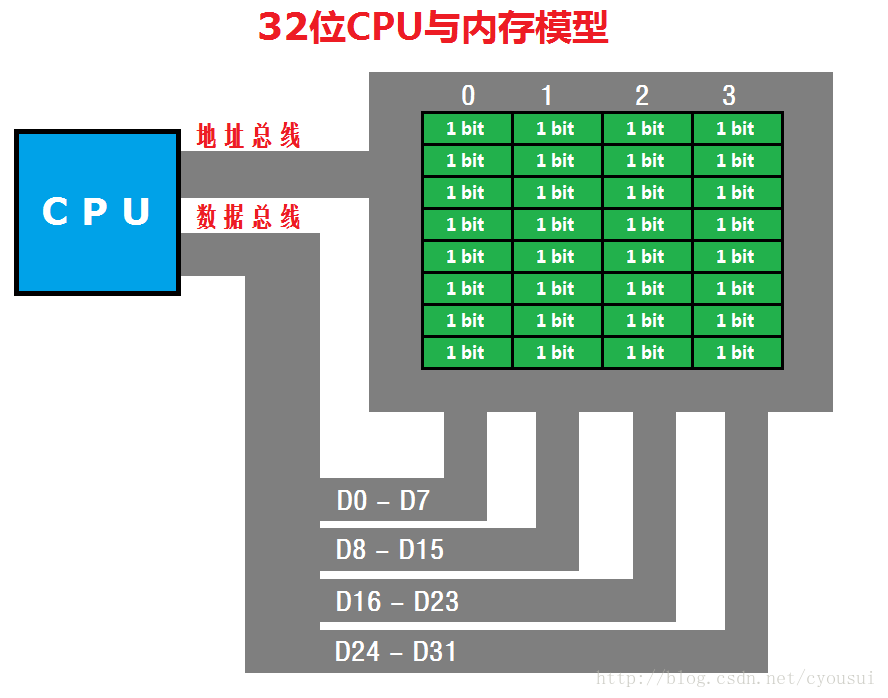
　　相信学过汇编的朋友都很熟悉这张图，这张图就是CPU与内存如何进行数据交换的模型，其中，左边蓝色的方框是CPU，右边绿色的方框是内存，内存上面的0～3是内存地址。这里我们这张图是以32位CPU作为代表，我们都知道，32位CPU是以双字（DWORD）为单位进行数据传输的，也正因为这点，造成了另外一个问题，那么这个问题是什么呢？这个问题就是，既然32位CPU以双字进行数据传输，那么，如果我们的数据只有8位或16位数据的时候，是不是CPU就按照我们数据的位数来进行数据传输呢？其答案是否定的，如果这样会使得CPU硬件变的更复杂，所以32位CPU传输数据无论是8位或16位都是以双字进行数据传输。

好了，有了上面的基础，就可以解释为什么需要内存对齐了。

1. 如果访问大小为一个字节的数据（eg : char 类型）,假设该数据放在内存地址1开始的位置，那么这个数据占用的内存地址为1，那么cpu通过一个指令周期，读出地址D0-D7 中的数据到寄存器中，然后通过移位指令移动相应的字节即可访问该数据。

2. 比如，一个int类型4字节的数据如果放在上图内存地址1开始的位置，那么这个数据占用的内存地址为1～4，那么这个数据就被分为了2个部分，一个部分在地址0～3中，另外一部分在地址4～7中，又由于32位CPU以双字进行传输，所以，CPU会分2次进行读取，一次先读取地址0～3中内容，再一次读取地址4～7中数据，最后CPU提取并组合出正确的int类型数据，舍弃掉无关数据。那么反过来，如果我们把这个int类型4字节的数据放在上图从地址0开始的位置会怎样呢？读到这里，也许你明白了，CPU只要进行一次读取就可以得到这个int类型数据了。没错，就是这样，这次CPU只用了一个周期就得到了数据，由此可见，对内存数据的摆放是多么重要啊，摆放正确位置可以减少CPU的使用资源。

由于上面解释的原因，gcc为代表的各种编译器默认采用了自然边界对齐的方式，那么什么是自然对齐，什么是对齐的内存地址呢， 请看下面的解释：

a. 一般计算机的内存是以字节（byte，等于8bit）为最小单元的。内存地址相当于从0开始的字节偏移数。如果一个内存地址是N的倍数，我们就说它是N字节对齐的（N-byte aligned）。

b. 对于C/C++中的基本数据类型，假设它的长度为n字节，那么该类型的变量会被编译器默认分配到n字节对齐的内存上。例如，char的长度是1字节，char类型变量的地址将是1字节对齐的（任意值均可）； int的长度是4字节，所以int类型变量将被分配到4字节对齐的地址上。这种默认情况下的变量对齐方式又称作自然对齐（naturally aligned）。

　　需要说明的是，以上对齐都是gcc编译器帮我们自动完成的，一般情况下，程序员不需要过多的关注上面的内容。但是，如果你是在做一些内存映射相关或者协议相关的工作的时候，你必须很清楚了解数据在内存中每一个字节的组织方式的时候，你就很有必要了解gcc编译器的默认对齐规则了，我们先从aligned和packed两个gcc属性说起.

本篇转载和参考资料：

http://blog.csdn.net/suifengpiao_2011/article/details/47260085

http://blog.shengbin.me/posts/gcc-attribute-aligned-and-packed