[JZOJ6244]【NOI2019模拟2019.7.1】Trominoes 【计数】

Description

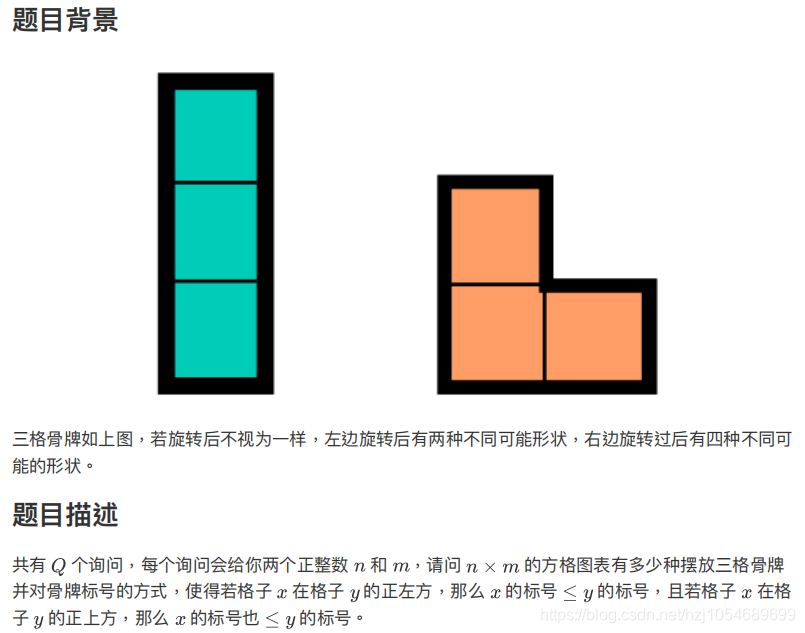
n,m<=10000

Solution

考虑暴力轮廓线DP，按顺序放骨牌

显然轮廓线长度为N+M

轮廓线也是单调的

1表示向上，0表示向右

N个1,M个0

只能放四种骨牌

四种转移写出来，就是

1000 0001

1110 0111

1010 0011

1100 0101

相当与一个1和后面3格的一个0换过来，中间不变

把模3相同的分组， 转换成只换相邻的10

再把它看作轮廓线，相当与每次只能放1×1的骨牌，问拓扑序个数

利用杨氏矩阵的钩子定理

就是矩阵大小的阶乘除以每个位置向右向下的位置个数和之积

最后再乘个组合数表示选的顺序

此时我们发现组合数约掉了，只剩下一个n×m的阶乘

直接计算即可。

Code

#include <bits/stdc++.h>
#define fo(i,a,b) for(int i=a;i<=b;++i)
#define fod(i,a,b) for(int i=a;i>=b;--i)
typedef long long LL;
const int mo=1000000007;
using namespace std;
int n,m,r,c[3][2],js[33333333];
LL ksm(LL k,LL n)
{
	LL s=1;
	for(;n;n>>=1,k=k*k%mo) if(n&1) s=s*k%mo;
	return s;
}
LL calc(int p)
{
	int n=c[p][0],m=c[p][1];
	LL s=1;
	fo(i,1,n+m-1)
	{
		LL nv=ksm(i,mo-2),ct=max(0,min(m-1,i-1)-max(0,i-n)+1);
		s=s*ksm(nv,ct)%mo;
	}
	return s;
}
int main()
{
	int t;
	cin>>t;
	int R=33333332;
	js[0]=1;
	fo(i,1,R) js[i]=js[i-1]*(LL)i%mo;
	while(t--)
	{
		cin>>n>>m;
		memset(c,0,sizeof(c));
		fo(i,0,n-1) c[i%3][0]++;
		fo(i,n,n+m-1) c[i%3][1]++;
		r=max(max(c[0][0]*c[0][1],c[1][0]*c[1][1]),c[2][0]*c[2][1]);
		LL v=1;
		int e=c[0][0]*c[0][1]+c[1][0]*c[1][1]+c[2][0]*c[2][1];
		printf("%lld\n",calc(0)*calc(1)%mo*calc(2)%mo*js[e]%mo);
	}
}