爬虫中GET方法应用基本模型

根据get方法，更改界面url从而获取信息

GET请求URL附带查询参数

POST请求保存在form表单中

分析百度贴吧url特点：

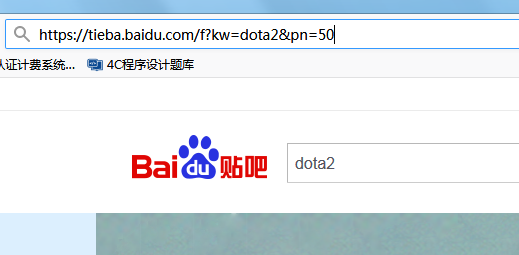
分析url https://tieba.baidu.com/f是贴吧总的url，？后是get请求，kw=xxx,&后是页码信息

爬取百度贴吧对应内容信息：

#python3
import urllib
import urllib.request
import urllib.response
import urllib.parse

def tieBarSpider(url,beginPage,endPage):
    """
        作用：负责处理url，分配每个url去发送请求
        url：需要处理的url
        beginPage：爬虫执行的起始页面
        endpage：爬虫执行的截止页面
    :return:
    """
    for page in range(beginPage,endPage):
        pn = (page-1)*50

        fileName = "第" + str(page) + "页"
        fullUrl = url + "&pn=" + str(pn)
        #print(fullUrl)
        html = loadHtmls(fullUrl)
        #将爬到的html页面保存到本地
        writeFiles(html,fileName)
        print("aleady：%s"%fileName)

def loadHtmls(fullUrl):
    """
        作用：根据url发送请求，获取服务器响应
        fullUrl：完整的每页的url
    :return:
    """
    #添加User-Agent头,伪装成浏览器访问
    headers = {'User-Agent': 'Mozilla/5.0 (Windows NT 6.1; WOW64; rv:23.0) Gecko/20100101 Firefox/23.0'}

    request = urllib.request.Request(fullUrl,headers=headers)

    reponse = urllib.request.urlopen(request)

    return reponse.read().decode()

#选择将爬取到的页面保存到本地
def writeFiles(html,filename):
    """
        功能：将爬取到的页面保存到本地
        html：页面html源码
        filename：保存到本地的名字
    :return:
    """
    #下面语句相当于
    # f = open(filename,'w')
    # f.write(html)
    # f.close()
    with open(filename,'w') as f:
        f.write(html)

    print('-'*20)

if __name__ == '__main__':

    #初始页url构建
    url = "https://tieba.baidu.com/f?"
    keyword = input("请输入要爬取的贴吧内容：")
    beginPage = int(input("BeginPage："))
    endPage = int(input("EndPage:"))
    #转码为url编码,urlencode()接受的是一个字典
    kw = urllib.parse.urlencode({"kw":keyword})
    fullUrl = url + kw

    tieBarSpider(fullUrl,beginPage,endPage+1)