线性规划(Simplex单纯形)与对偶问题

线性规划

首先一般所有的线性规划问题我们都可以转换成如下标准型：

但是我们可以发现上面都是不等式，而我们计算中更希望是等式，所以我们引入这个新的概念：松弛型：

很显然我们最后要求是所有的约束左边的变量都不小于0。而求解这类问题，我们又有一套十分便利的模型算法：单纯形

基变量：松弛型等式左边的所有变量

非基变量：松弛型等式右侧的所有变量

基本解：一组基变量和非基变量蕴含着一组基本解，即所有的非基变量都为0，基变量都为等式右侧的常数项（这里要求常数项为正，为负时我们后面讨论）

算法原理：

可证线性规划的解空间是一个凸形区域，也就是说全局最优解只有一个，或者同时有多个平行的最优解。由上性质我们可以知道，局部最优解一定时全局最优解，这就是单纯形的算法思想。

算法过程：

转轴操作：选择一个基变量和非基变量，将其互换

simplex操作：主过程，从一个基本解出发，经过一系列的转轴操作，找到最优解

举例：

求解如下问题：

第一步：互换x1与x6

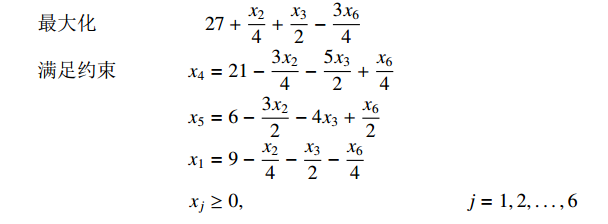
第二步：互换x3与x5

第三步：互换x2与x3

此时我们得到的基本解：（x1, x2, x3, x4, x5, x6） = (8, 4, 0, 18, 0, 0)，易验证就是最后的最优解

算法伪代码：

 def Simplex(A, b, c):
     initialization(A, b, c)
     while there is e that Ce > 0 do:
         find the index l that Ale > 0 and minimizes bi/Ale
         if all l, Ale <= 0 then:
             return Unbounded
         else:
             pivot(A, b, c, l, e)

其中我们发现有一个“initialization”函数就是用于处理我们的bi<0的情况，它的做法是引入一个辅助的线性规划：

这样经过一次转轴操作以后，第l个约束变为：

其余的变为：

易知此时对于新的bi满足都不小于0

对偶问题

定义：

用矩阵表示更形象，而且也更利于我们后期的计算与理解：

因此我们在面对这类问题时可以考虑它们之间的相互转化。这里不加证明给出一下定理：

互为对偶问题的两组最优解相等

后续更新Simplex算法的python实现……