[CSP-S模拟测试]:Emotional Flutter（贪心）

题目传送门（内部题51）

---

输入格式

第一行一个整数$t$表示数据组数。
每组数据的第一行有三个整数$s,k,n$。
第二行有$n$个整数$A_1,A_2,...,A_n$，依次表示黑白条的长度。

---

输出格式

若能通过输出$"TAK"$，否则输出$"NIE"$。

---

样例

样例输入：

2
2 8 7
2 5 6 3 2 1 2
2 8 4
1 6 7 4

样例输出：

TAK
NIE

---

数据范围与提示

样例解释：

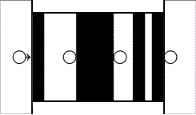
数据范围：

$30\%$的数据，$n\leqslant 1300$；
$50\%$的数据，$n\leqslant 22,000$；
$100\%$的数据，$2\leqslant n\leqslant 500,000,1\leqslant s<k\leqslant {10}^9,1\leqslant A_i\leqslant {10}^9,1\leqslant t\leqslant 10$。
数据有梯度。输入文件较大请使用读入优化。

---

题解

其实就是一个贪心，主要是策略很难想。

首先来处理脚的长度，我们可以将所有的黑块都延长$s$，所有的白块左端点向右移动$s$，这样就相当与忽略了脚的长度。

然后会有一些特判的情况，对于我的贪心策略，我们只需要用到当一个黑块长度大于$k$时，肯定跳不过去，所以直接输出$"NIE"$即可。

现在来讲对于一般情况，我是如何判断的。

首先，将所有的黑块的左端点和右端点分别$\mod k$，那么我们是不能在这段区间进行起跳的；如果出现$\mod k$完之后右端点小于左端点，那么区间$[0,r]$和区间$[l,k-1]$是不能起跳的。

之后我们只需要将所有的不能跳的区间排个序，然后我们只需要找到一个可以起跳的点即可。

细节比较多，慢慢调吧……

时间复杂度：$\Theta(n\log n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec{long long l,r;}e[10000000];
long long s,k,n;
long long sum[5000001];
long long lft[5000001],rht[5000001],wsq;
int top;
bool flag;
bool cmp(rec a,rec b){return a.l==b.l?a.r<b.r:a.l<b.l;}
int main()
{
	int T;scanf("%d",&T);
	while(T--)
	{
		scanf("%lld%lld%lld",&s,&k,&n);
		top=flag=wsq=0;
		for(int i=1;i<=n;i++)
		{
			long long a;
			scanf("%lld",&a);
			if(i&1)a+=s;
			else{a-=s;a%=k;}
			if(a>k)flag=1;
			sum[i]=sum[i-1]+a;
			if(i&1)
			{
				lft[i]=sum[i-1]+1;
				rht[i]=sum[i]-1;
			}
		}
		if(((n&1)&&sum[n]<=k)||((!(n&1))&&sum[n-1]<=k)){puts("TAK");continue;}
		if(flag){puts("NIE");continue;}
		for(int i=1;i<=n;i+=2)
		{
			lft[0]=lft[i]%k;
			rht[0]=rht[i]%k;
			if(rht[0]<lft[0])
			{
				e[++top]=(rec){0,rht[0]};
				e[++top]=(rec){lft[0],k-1};
			}
			else e[++top]=(rec){lft[0],rht[0]};
		}
		sort(e+1,e+top+1,cmp);
		if(e[1].l){puts("TAK");goto nxt;}
		for(int i=1;i<=top;i++)
		{
			if(wsq+1<e[i].l){puts("TAK");goto nxt;}
			wsq=max(wsq,e[i].r);
		}
		if(wsq<k-1){puts("TAK");continue;}
		puts("NIE");
		nxt:;
	}
	return 0;
}

---

rp++