[CSP-S模拟测试]:线性代数（模拟）

题目传送门（内部题113）

---

输入格式

　　第一行一个正整数$n$。
　　接下来$n$行，每行$n$个整数，描述$C$矩阵。保证输入的是一个林先森矩阵。

---

输出格式

　　若不可能实现，则输出一行$Impossible$；否则，输出一行一个仅包含$\{U,D,L,R\}$的字符串，表示一个$typ$参数的序列。你的序列长度不能超过$10^6$。若不需要进行任何操作，请将该序列留空。

---

样例

样例输入1：

2
1 2
3 0

样例输出1：

Impossible

样例输入2：

3
3 2 5
4 1 8
6 7 0

样例输出2：

UULDLU

---

数据范围与提示

　　本题采用子任务评分。仅当你通过一个子任务下所有测试点时，你才能获得该子任务的分数。
　　对于所有数据，$1\leqslant n\leqslant 50$。
　　$1.$（$30$分）$n\leqslant 3$。
　　$2.$（$30$分）$n\leqslant 10$。
　　$3.$（$40$分）没有特殊限制。

---

题解

其实就是一个大模拟。

我们考虑从小到大填，也就是先填好右下角，每一行从右到左填，从下到上依次填好每一行，直到最后两行不管。

先说怎么填好每一行。

首先，先填好每一行$3\sim n$的每一个数，方法很简单，不再赘述。

$1,2$位置需要一起填，具体方法我们可以先想办法将其变成如下图所示的情况$\downarrow$

上图中，黑色为已经填好的块和边界，橙色为准备填的两个块，这样我们只需要将$0$向左再向上移动即可移动成下图的状态$\downarrow$

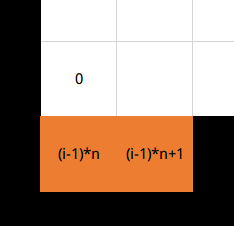
剩余$1,2$两行没有填好时只需要按上面填每行的$1,2$的方法填补即可。

最后剩下左上角一个$2\times 2$的方格时判断即可。

时间复杂度：$\Theta(n^3)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n;
int Map[55][55],sec[55][55];
bool vis[55][55];
pair<int,int> pos[10000];
int top;
char ans[10000010];
int dis(int x,int y,int x2,int y2){return abs(x-x2)+abs(y-y2);}
void U()
{
	swap(Map[pos[0].first][pos[0].second],Map[pos[0].first-1][pos[0].second]);
	swap(pos[0],pos[Map[pos[0].first][pos[0].second]]);ans[++top]='U';
	if(top>1e6){puts("Impossible");exit(0);}
}
void D()
{
	swap(Map[pos[0].first][pos[0].second],Map[pos[0].first+1][pos[0].second]);
	swap(pos[0],pos[Map[pos[0].first][pos[0].second]]);ans[++top]='D';
	if(top>1e6){puts("Impossible");exit(0);}
}
void L()
{
	swap(Map[pos[0].first][pos[0].second],Map[pos[0].first][pos[0].second-1]);
	swap(pos[0],pos[Map[pos[0].first][pos[0].second]]);ans[++top]='L';
	if(top>1e6){puts("Impossible");exit(0);}
}
void R()
{
	swap(Map[pos[0].first][pos[0].second],Map[pos[0].first][pos[0].second+1]);
	swap(pos[0],pos[Map[pos[0].first][pos[0].second]]);ans[++top]='R';
	if(top>1e6){puts("Impossible");exit(0);}
}
int judge(int x,int y)
{
	if(pos[0]==make_pair(x,y+1))return 1;
	if(pos[0]==make_pair(x,y-1))return 2;
	if(pos[0]==make_pair(x-1,y))return 3;
	if(pos[0]==make_pair(x+1,y))return 4;
	return 0;
}
void change(int x,int y)
{
	while(1)
	{
		if(judge(x,y))break;
		int flag=0;
		if(pos[0].first-1==x&&pos[0].second==y)goto nxt1;
		if(pos[0].first>1&&dis(x,y,pos[0].first,pos[0].second)>dis(x,y,pos[0].first-1,pos[0].second)&&!vis[pos[0].first-1][pos[0].second]){U();flag=1;}
		nxt1:;
		if(pos[0].first+1==x&&pos[0].second==y)goto nxt2;
		if(pos[0].first<n&&dis(x,y,pos[0].first,pos[0].second)>dis(x,y,pos[0].first+1,pos[0].second)&&!vis[pos[0].first+1][pos[0].second]){D();flag=1;}
		nxt2:;
		if(pos[0].first==x&&pos[0].second-1==y)goto nxt3;
		if(pos[0].second>1&&dis(x,y,pos[0].first,pos[0].second)>dis(x,y,pos[0].first,pos[0].second-1)&&!vis[pos[0].first][pos[0].second-1]){L();flag=1;}
		nxt3:;
		if(pos[0].first==x&&pos[0].second+1==y)goto nxt4;
		if(pos[0].second<n&&dis(x,y,pos[0].first,pos[0].second)>dis(x,y,pos[0].first,pos[0].second+1)&&!vis[pos[0].first][pos[0].second+1]){R();flag=1;}
		nxt4:;
		if(!flag)break;
	}
}
void move(int k,int x,int y)
{
	int opt=judge(x,y);
	switch(k)
	{
		case 1:
			if(opt==1){U();L();D();}
			if(opt==2){U();R();D();}
			if(opt==3)D();
			if(opt==4)
			{
				if(y>1){L();U();U();R();D();}
				else{R();U();U();L();D();}
			}
		break;
		case 2:
			if(opt==1)
			{
				if(vis[x+1][y+1]){U();L();D();D();R();U();L();U();R();D();D();L();U();}
				else{D();L();U();}
			}
			if(opt==2){D();R();U();}
			if(opt==3)
			{
				if(y<n){R();D();}
				else{L();D();D();R();U();}
			}
			if(opt==4)U();
		break;
		case 3:
			if(opt==1){U();L();L();D();R();}
			if(opt==2)R();
			if(opt==3){L();D();R();}
			if(opt==4){L();U();R();}
		break;
		case 4:
			if(opt==1)L();
			if(opt==2)
			{
				if(x>1){U();R();R();D();L();}
				else
				{
					if(vis[x+1][y+1]){R();D();R();U();L();D();R();U();L();L();D();R();R();U();L();}
					else{D();R();R();U();L();}
				}
			}
			if(opt==3){R();D();L();}
			if(opt==4)
			{
				if(vis[x+1][y+1]){L();U();}
				else{R();U();L();}
			}
		break;
	}
}
void move(int x,int y)
{
	int res=sec[x][y];
	while(pos[res]!=make_pair(x,y))
	{
		bool flag=0;
		if(pos[res].first>1&&dis(x,y,pos[res].first,pos[res].second)>dis(x,y,pos[res].first-1,pos[res].second)&&!vis[pos[res].first-1][pos[res].second])
		{change(pos[res].first,pos[res].second);move(1,pos[res].first,pos[res].second);flag=1;}
		if(pos[res].first<n&&dis(x,y,pos[res].first,pos[res].second)>dis(x,y,pos[res].first+1,pos[res].second)&&!vis[pos[res].first+1][pos[res].second])
		{change(pos[res].first,pos[res].second);move(2,pos[res].first,pos[res].second);flag=1;}
		if(pos[res].second>1&&dis(x,y,pos[res].first,pos[res].second)>dis(x,y,pos[res].first,pos[res].second-1)&&!vis[pos[res].first][pos[res].second-1])
		{change(pos[res].first,pos[res].second);move(3,pos[res].first,pos[res].second);flag=1;}
		if(pos[res].second<n&&dis(x,y,pos[res].first,pos[res].second)>dis(x,y,pos[res].first,pos[res].second+1)&&!vis[pos[res].first][pos[res].second+1])
		{change(pos[res].first,pos[res].second);move(4,pos[res].first,pos[res].second);flag=1;}
		if(!flag)break;
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			scanf("%d",&Map[i][j]);sec[i][j]=(i-1)*n+j-1;
			pos[Map[i][j]]=make_pair(i,j);
		}
	for(int i=n;i>2;i--)
		for(int j=n;j;j--)
		{
			move(i,j);
			vis[i][j]=1;
		}
	for(int j=n;j>1;j--)
	{
		move(2,j);vis[2][j]=1;
		move(1,j);vis[1][j]=1;
	}
	if(pos[0]!=make_pair(1,1)){swap(Map[1][1],Map[2][1]);ans[++top]='U';}
	printf("%s",ans+1);
	return 0;
} 

---

rp++