[bzoj 1005][HNOI 2008]明明的烦恼（prufer数列+排列组合）

题目：http://www.lydsy.com/JudgeOnline/problem.php?id=1005

分析：

首先prufer数列：http://baike.baidu.com/view/10474884.htm?fr=aladdin

从百度百科中我们可以弄出prufer数列的几个性质：

1、prufer数列与节点编号1~n的无根树一一对应

2、prufer数列的长度为n-2

3、prufer数列中每个数出现次数==这个数对应的节点在无根树中的度数-1（注意叶节点肯定不在prufer数列中的）

由性质1我们可以将问题转化成求prufer数列的个数，而对度数的要求也由性质3可以转换成堆prufer中数字出现个数的要求，这就转换成了基础的高中排列组合题了。换言之，让你从1~n中挑出n-2个数（可以重复也可以不挑）组成一个数列，一些数字的出现个数固定，一些数字的出现个数随意，问数列的种数。

按高中排列组合的思想，先考虑“捆绑”的，即出现个数固定的数字。设读入的度数分别为d1,d2,d3,……,dm，

则个数为C(n-2,d1-1)*C(n-2-(d1-1),d2-1)*…… 化简一下就可以得到：

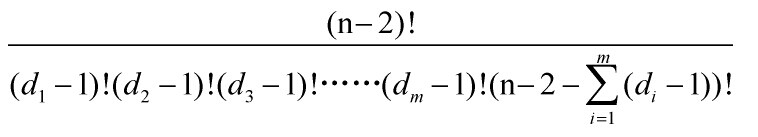
然后考虑那些剩下的，则为：

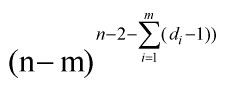
然后结果就是两个相乘，计算的时候分解质因数就行