洛谷 [T21776] 子序列

题目描述

你有一个长度为 \(n\) 的数列 \(\{a_n\}\) ，这个数列由 \(0,1\) 组成，进行 \(m\) 个的操作：

\(1\ l\ r\) ：把数列区间$ [l,r]$ 内的所有数取反。即 \(0\) 变成 \(1\) ，\(1\) 变成 \(0\) 。

\(2\ l\ r\) ：询问数列在区间 \([l, r]\) 内共有多少个本质不同的子序列。

输入输出格式

输入格式：

第一行包含两个整数 \(n,m\)，意义如上所述。

接下来一行包含 \(n\) 个数，表示数列 \(\{a_n\}\) 。

接下来 \(m\) 行，每行包含三个数，表示一个操作，操作格式如上所述。

输出格式：

对于每个询问，输出答案模 \(10^{9}+7\) 的结果。

思路

前置技能：

维护一个长度为 \(n\) 的 \(3*3\) 的 \(0/1\) 矩阵序列

1. 交换区间 \([l,r]\) 中所有矩阵的第一行和第二行

2. 查询区间 \([l,r]\) 中所有矩阵从左到右乘起来的结果

对于能快速合并的信息我们都可以用线段树来维护

比如和，积，最值， 矩阵乘法， bitset， hash值，线性基

还需要一个矩阵的结论：

对于 3*3 的 0/1 矩阵来说 两矩阵的第一二行交换，他们的乘积的第一二行也交换

所以可以对于交换的区间打 tag，用线段树维护

本题思路

考虑本质不同的子序列怎么求：

设 f(i,0) 表示i号位置以前的以0结尾的本质不同的子序列数目

设 f(i,1) 表示i号位置以前的以1结尾的本质不同的子序列数目

转移方程 ：

如果 i 号位置是 0 ，\(f(i,0) = f(i-1,0) + f(i-1,1) + 1 ; f(i, 1) = f(i-1, 1)\)

如果 i 号位置是 1 ，\(f(i,1) = f(i-1,0) + f(i-1,1) + 1 ; f(i, 0) = f(i-1, 0)\)

用矩阵加速，可得：

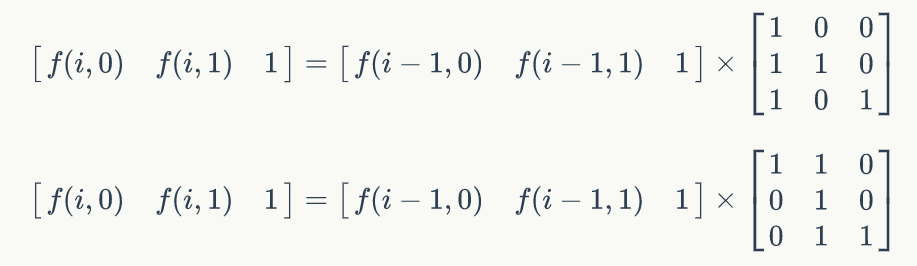
观察矩阵可得，对区间内序列取反，可以转化为把矩阵的前两行，前两列交换

可用线段树来维护

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define lson l, mid, rt<<1
#define rson mid+1, r, rt<<1|1
using namespace std;
const int MOD = 1e9 + 7;
int init() {
	int rv = 0, fh = 1;
	char c = getchar();
	while(c <'0' || c > '9') {
		if(c == '-') fh = -1;
		c=getchar();
	}
	while(c >= '0' && c <= '9') {
		rv=(rv<<1) + (rv<<3) + c- '0';
		c = getchar();
	}
	return fh * rv;
}
const int MAXN=100005;
struct Matrix{
	ll num[3][3];
	int col;
	Matrix() {
		col = 0;
		memset(num,0,sizeof(num));
	}
	void build(bool f){
		col=3;
		if(f) {
			num[0][0] = num[0][1] = num[1][1] = num[2][1] = num[2][2] = 1;
		}else {
			num[0][0] = num[1][0] = num[2][0] = num[1][1] = num[2][2] = 1;
		}
	}
	Matrix operator * (const Matrix &a) {
		Matrix ans;
		ans.col = col;
		for(int i = 0 ; i < col ; i++) {
			for(int j = 0 ; j < 3 ; j++) {
				for(int k = 0 ; k < 3 ; k++) {
					(ans.num[i][j] += num[i][k] * a.num[k][j]) %= MOD;
				}
			}
		}
		return ans;
	}
	void reserve() {
		for(int i = 0 ; i < 3 ; i++) {
			swap(num[0][i],num[1][i]);
		}
		for(int i = 0 ; i <3 ; i++) {
			swap(num[i][0], num[i][1]);
		}
	}
	void print() {
		for(int i = 0 ; i<=col ;i++) {
			for(int j = 0 ; j < 3 ; j++) {
				printf("%d ",num[i][j]);
			}
			cout<<endl;
		}
	}
};
struct SGT{
	Matrix sum[MAXN<<2];
	bool tag[MAXN<<2];
	void PushUp(int rt) {
		sum[rt] = sum[rt<<1] * sum[rt<<1|1];
	}
	void build(int l, int r,int rt) {
		if(l==r) {
			bool f=init();
			sum[rt].build(f);
			return;
		}
		int mid = (l + r) >>1;
		build(lson);
		build(rson);
		PushUp(rt);
	}
	void PushDown(int rt) {
		if(tag[rt]) {
			tag[rt<<1] = !tag[rt<<1] ;
			tag[rt<<1|1] = !tag[rt<<1|1];
			sum[rt<<1].reserve();
			sum[rt<<1|1].reserve();
			tag[rt]=0;
		}
	}
	void Update(int L, int R, int l, int r, int rt) {
		if(L <= l && r <= R) {
			tag[rt]=!tag[rt];
			sum[rt].reserve();
			return;
		}
		PushDown(rt);
		int mid = (l + r) >>1;
		if(L <= mid) Update(L, R, lson);
		if(mid < R) Update(L, R, rson);
		PushUp(rt);
	}
	Matrix Query(int L, int R, int l, int r, int rt) {
		if(L <= l && r <= R) {
			return sum[rt];
		}
		PushDown(rt);
		int mid = (l + r) >>1;
		Matrix ans;
		ans.col = 3;
		ans.num[0][0] = ans.num[1][1] = ans.num[2][2] = 1;//ans.print();
		if(L <= mid) ans = ans * Query(L, R, lson);
		if(mid < R) ans = ans * Query(L, R, rson);
		PushUp(rt);
		return ans;
	}
}sgt;
int n,m;
int main() {
	freopen("in.txt", "r", stdin);
	n=init();m=init();
	sgt.build(1,n,1);
	for(int i = 1 ; i <= m ; i++) {
		int t = init(), l = init(), r = init();
		if(t == 1) {
			sgt.Update(l, r, 1, n, 1);
		}else {
			Matrix ans;
			ans.col = 1;ans.num[0][2] = 1;
			ans = ans * sgt.Query(l, r, 1, n, 1);
			//sgt.Query(l, r, 1, n, 1).print();
			printf("%lld\n",(ans.num[0][0] + ans.num[0][1])%MOD);
		}
	}
	fclose(stdin);
	return 0;
}