codeforces #463

D(树上倍增)

题意：

　　刚开始有一个点1，权值为0。

　　接下来有q个操作，每个操作有两种：

　　1 R W：新加一个点，这个点的权值为W，这个点的父亲是R

　　2 R X：在从点R到1的路径上，取出从R开始的不降单调栈，问从栈底到栈顶这么多元素，最多能取出多少个点，使得这些点的点权和<=X

　　强制在线

　　q<=400000

分析：

　　虽然这个树的形态不是固定的，但仍旧可以倍增，因为每次加的都是叶子节点，对上面的形态是不改变的

　　我们可以先倍增求出每个点的最上方的不必它点权小的点fa

　　然后根据这个fa信息组成一个新的森林，再在这上面倍增去回答点权和<=X的询问

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn=4e5;
 int fa[maxn+][],g[maxn+][];
 ll mx[maxn+][],sum[maxn+][];
 int dep[maxn+];
 int n;
 int last=;
 int main()
 {

     int T;
     scanf("%d",&T);
     n=;
     mx[][]=;
     dep[]=;
     while(T--)
     {
         int op;
         long long r,w;
         scanf("%d%lld%lld",&op,&r,&w);

         r^=last,w^=last;
                 //printf("operation : %d %lld %lld\n",op,r,w);
         if(op==)
         {
             ++n;
             mx[n][]=w;
             fa[n][]=r;
             int x=fa[n][];
             for(int i=;i>=;--i)
                 if(mx[x][i]<w) x=fa[x][i];
            // if(n==3) printf("ce %d\n",x);

             //printf("ce %d %d\n",n,x);
             for(int i=;i<=;++i)
             {
                 mx[n][i]=max(mx[n][i-],mx[fa[n][i-]][i-]);
                 fa[n][i]=fa[fa[n][i-]][i-];
             }
             g[n][]=x;
             dep[n]=dep[x]+;
             sum[n][]=w;
             for(int i=;i<=;++i)
             {
                 sum[n][i]=sum[n][i-]+sum[g[n][i-]][i-];
                 g[n][i]=g[g[n][i-]][i-];
             }
         }
         else
         {
             last=;
             int x=r;
             for(int i=;i>=;--i)
             {
                 //printf("%d : %d ",i,sum[x][i]);
                 if(sum[x][i]<=w)
                 {
                     w-=sum[x][i];
                     x=g[x][i];
                 }
                 //printf("%d\n",x);
             }
             //printf("x %d\n",x);
             last=dep[r]-dep[x];
             printf("%d\n",last);
         }
     }
     //printf("ce : %d\n",sum[2][0]);
     return ;
 }

E(斯特林数下降幂)

题意：

　　

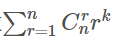
　　给定n,k，求这个式子的值n<=1e9,k<=5000

分析：

　　对于x^k这个可以用第二类斯特林数下降幂展开并化简，最后可以得出一个简单的式子

　　因为k比较小，所以可以直接递推求第二类斯特林数

 #include<bits/stdc++.h>
 using namespace std;

 const int N=,P=1e9+;

 int S[N][N];

 inline int Pow(int x,int y){
   int ret=;
   for(;y;y>>=,x=1LL*x*x%P) if(y&) ret=1LL*ret*x%P;
   return ret;
 }

 inline int A(int n,int j){
   int ret=;
   for(int i=;i<j;i++)
     ret=1LL*ret*(n-i)%P;
   return ret;
 }

 int main(){
   S[][]=;
   for(int i=;i<=;i++){
     for(int j=;j<=i;j++)
       S[i][j]=(S[i-][j-]+1LL*j*S[i-][j])%P;
   }
   int ans=;
   int n,k; scanf("%d%d",&n,&k);
   for(int j=;j<=k && j<=n;j++)
     ans=(ans+1LL*S[k][j]*A(n,j)%P*Pow(,n-j))%P;
   printf("%d\n",ans);
   return ;
 }

F(树上动态凸包)

题意：

　　有一个n个点的树，每个点有两个属性a和b，对于一个点u，dp[u]=min(dp[v]+a[u]*b[v])，其中v是u子树中的点，求出每个点的dp值

　　n<=100000

分析：

　　直接dp肯定会超时

　　这个如果不是树而是一条链，那是可以用凸包来优化的

　　如果是一颗树的话，那么自然而然想到就涉及到几个子树的凸包的合并

　　这个可以采取启发式合并，把小的凸包里的点往大的凸包里的点插，询问就在凸包上二分

　　凸包用set来维护

　　注意在set上二分的姿势

　　时间复杂度O(nlog^2n)

 #include<bits/stdc++.h>
 using namespace std;
 #define mp make_pair
 const int maxn=1e5;
 typedef long long ll;
 const ll inf=100000000000000000LL;
 typedef pair<int,ll> Point;
 ll a[maxn+],b[maxn+],dp[maxn+];
 vector<int> g[maxn+];
 int n;
 set<Point> s[maxn+];
 double cross(Point a,Point b,Point c)
 {
     ll x=b.first-a.first,y=b.second-a.second;
     ll xx=c.first-b.first,yyy=c.second-b.second;
     return (double)x*yyy-(double)y*xx;
 }
 void insert(set<Point> &s,Point p)
 {
     set<Point>::iterator it=s.lower_bound(p);
     set<Point>::iterator jt=it;
     if(it!=s.begin()) --jt;
     if(it!=s.begin()&&it!=s.end()&&cross(*jt,p,*it)<=) return;
     if(it!=s.begin())
     {
         it=jt;
         while(it!=s.begin())
         {
             jt=it;
             --jt;
             if(cross(*jt,*it,p)<=) s.erase(it--);else break;
         }
     }
     jt=s.lower_bound(p);
     if(jt!=s.end()) it=jt++;
     while(jt!=s.end())
     {
         if(cross(p,*it,*jt)<=) s.erase(it++);else break;
         jt=it;
         ++jt;
     }
     s.insert(p);
 }
 ll query(set<Point> &s,ll k)
 {
     if(s.empty()) return ;
     ll l=s.begin()->first,r=s.rbegin()->first,mid;
     while(l<r)
     {
         mid=(l+r+)>>;
         set<Point>::iterator it=s.lower_bound(mp(mid,-inf)),jt=it--;
         if(k*(jt->first-it->first)>=jt->second-it->second) l=mid;else r=mid-;
     }
    Point res=*s.lower_bound(mp(l,-inf));
     return (-k)*res.first+res.second;
 }
 void dfs(int k,int fa)
 {
     for(auto u:g[k])
     {
         if(u==fa) continue;
         dfs(u,k);
         if(s[k].size()<s[u].size()) s[k].swap(s[u]);
         for(auto x:s[u])
             insert(s[k],x);
         set<Point>().swap(s[u]);
     }
     dp[k]=query(s[k],-a[k]);
     insert(s[k],mp(b[k],dp[k]));

 }
 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;++i) scanf("%lld",&a[i]);
     for(int i=;i<=n;++i) scanf("%lld",&b[i]);
     for(int i=;i<n;++i)
     {
         int u,v;
         scanf("%d%d",&u,&v);
         g[u].push_back(v),g[v].push_back(u);
     }
     dfs(,);
     for(int i=;i<=n;++i) printf("%lld ",dp[i]);
     return ;
 }

G(回文树)

待填坑