10.12NOIP模拟题(1)

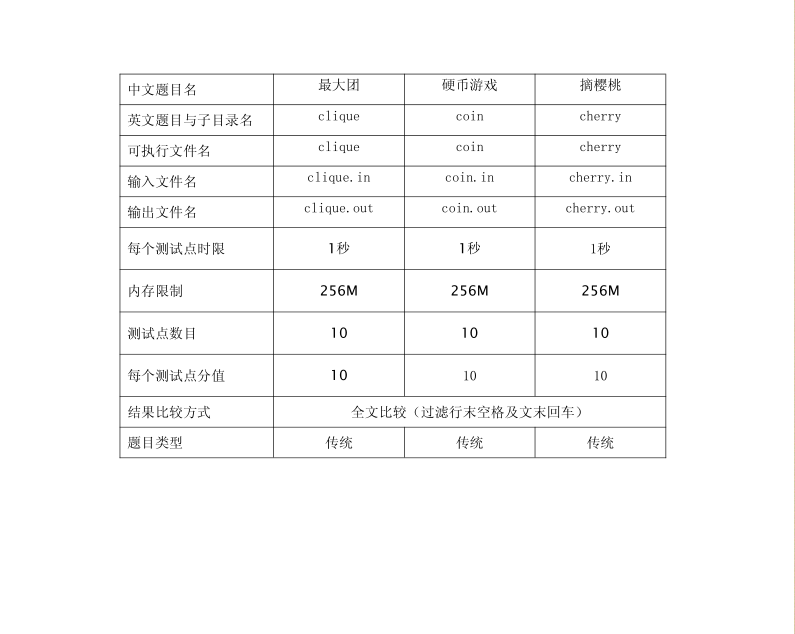
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>

#define N 2001

using namespace std;
int n,m,ans,cnt;
int vis[N],w[N],x[N],deep[N];
int e[N][N];
queue<int>q;

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

void bfs(int now)
{
    while(!q.empty()) q.pop();
    memset(vis,,sizeof vis);
    memset(deep,,sizeof deep);
    q.push(now);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        ans=max(ans,deep[u]+);
        for(int i=;i<=n;i++)
        {
            if(u==now&&e[i][now])
            {
                deep[i]=deep[now]+;
                q.push(i);
            }
            else if(deep[i]==deep[u] && e[u][i])
            {
                deep[i]=deep[u]+;
                q.push(i);
            }
        }
    }
}

int main()
{
    freopen("clique.in","r",stdin);
    freopen("clique.out","w",stdout);
    int tmp;
    n=read();
    for(int i=;i<=n;i++) x[i]=read(),w[i]=read();
    for(int i=;i<=n;i++) for(int j=;j<=n;j++)
    {
        if(i==j) continue;
        tmp=x[i]-x[j];
        if(tmp<) tmp=-tmp;
        if(tmp>=w[i]+w[j]) e[i][j]=e[j][i]=;
    }
    for(int i=;i<=n;i++)
    bfs(i);
    printf("%d\n",ans);
    return ;
}

20暴力23333

/*
将点(xi,wi)看成区间(xi-wi,xi+wi)，绝对值去掉移项
那么两个点有连边当且仅当两个区间没有公共点
最多的不重合的区间数就是最大团的点数
删去所有包含其它区间的区间，在剩下的区间中每次贪心取一个能取的坐标最小的区间。
*/
#include<algorithm>
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=;
int n;
struct zhw{
    int l,r;
    friend bool operator <(zhw a,zhw b)
    {
        return  a.r<b.r||(a.r==b.r&&a.l>b.l);
    }
}a[maxn];
int x,w,l,r;
int main()
{
    freopen("clique.in","r",stdin);
    freopen("clique.out","w",stdout);
    scanf("%d",&n);
    for(int i=;i<=n;++i)
    {
        scanf("%d%d",&x,&w);
        a[i].l=x-w,a[i].r=x+w;
    }
    sort(a+,a+n+);
    int pos=a[].r,ans=;
    for(int i=;i<=n;++i)
    {
        if(a[i].l>=pos)ans++,pos=a[i].r;
    }
    printf("%d",ans);
    fclose(stdin);fclose(stdout);
    return ;
}

/*
可以对硬币的编号取模k，这样就分成了k组
每一组中，若有偶数堆硬币那这一组硬币可以全部拿走。
若有奇数堆硬币那一定会有一堆剩余
而且剩余的一定是编号为奇数的那一堆（自己写一下就能发现一定是编号为奇数的剩余）
同样把这一组的所有硬币价值加起来，再减去这一堆中编号为奇数，并且价值最小的那一堆即可。
*/
#include <cstdio>
#include <iostream>

#define ll long long 

using namespace std;
int n,k;
ll a[];

int main()
{
      freopen("coin.in","r",stdin);
      freopen("coin.out","w",stdout);

      scanf("%d%d",&n,&k);k--;
      for (int i=;i<n;i++) scanf("%lld",&a[i]);

      ll ret=;
    for (int i=;i<=k;i++)
    {
        ll mini=1e9,tot=;
          for (int j=i;j<n;j+=k+)
        {
              tot^=;
            if (tot) mini=min(mini,a[j]);
            ret+=a[j];
          }
          ret-=tot*mini;
    }
    cout<<ret;
}

/*
水水的dp
*/
#include<iostream>
#include<cstring>
#include<cstdio>

#define N 1007

using namespace std;
int n,t;
int v[N],sum[N];
int f[N];

int main()
{
    freopen("cherry.in","r",stdin);
    freopen("cherry.out","w",stdout);
    scanf("%d%d",&n,&t);
    for(int i=;i<=n;++i)
    scanf("%d",&v[i]),sum[i]=sum[i-]+v[i];
    memset(f,/,sizeof(f));
    f[]=;
    for(int i=;i<=n;++i)
        for(int j=;j<=i;j++)
            f[i]=min(f[i],f[j-]+(sum[i]-sum[j-]-t)*(sum[i]-sum[j-]-t));
    printf("%d",f[n]);
    return ;
}