算法笔记_064:蓝桥杯练习 操作格子（Java）

目录

1 问题描述

2 解决方案

 

---

1 问题描述

问题描述

有n个格子，从左到右放成一排，编号为1-n。

共有m次操作，有3种操作类型：

1.修改一个格子的权值，

2.求连续一段格子权值和，

3.求连续一段格子的最大值。

对于每个2、3操作输出你所求出的结果。

输入格式

第一行2个整数n，m。

接下来一行n个整数表示n个格子的初始权值。

接下来m行，每行3个整数p,x,y，p表示操作类型，p=1时表示修改格子x的权值为y，p=2时表示求区间[x,y]内格子权值和，p=3时表示求区间[x,y]内格子最大的权值。

输出格式

有若干行，行数等于p=2或3的操作总数。

每行1个整数，对应了每个p=2或3操作的结果。

样例输入

4 3
1 2 3 4
2 1 3
1 4 3
3 1 4

样例输出

6
3

数据规模与约定

对于20%的数据n <= 100，m <= 200。

对于50%的数据n <= 5000，m <= 5000。

对于100%的数据1 <= n <= 100000，m <= 100000，0 <= 格子权值 <= 10000。

---

2 解决方案

花了一上午的时间把线段树整明白，然后把写好的代码放到蓝桥杯练习系统里面测试时，运行结果依旧是超时，而且我用同样的代码反复提交了三四次，分数也都竟然都不一样，分别是30,40,50。我也是无语了...

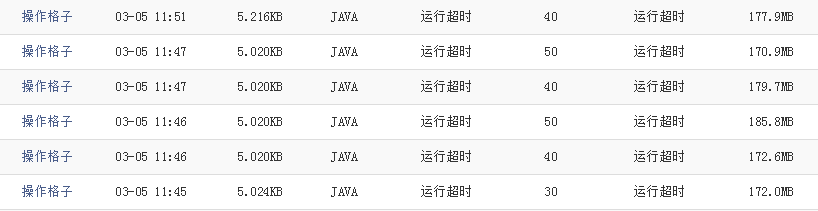
虽然这题没能得到100分，我猜测可能与Java和C/C++语言之间的编译运行性能有关，导致用同样的方法，Java语言运行时间要长的多。

如果有哪位同学看出下面的代码不是语言之间的差异，而是楼主我自己的代码问题，还希望路过的同学不吝赐教呀~

关于线段树，具体的理解可以参考文末的参考资料，参考资料给的文章个人感觉对于线段树的讲解很清楚，唯一的不足之处是文中对于完全二叉树的概念理解有点错误，但是不影响我们对于线段树的理解哦。

下面附一点该文章对于线段树的概念介绍：

线段树，类似区间树，它在各个节点保存一条线段（数组中的一段子数组），主要用于高效解决连续区间的动态查询问题，由于二叉结构的特性，它基本能保持每个操作的复杂度为O(logn)。

线段树的每个节点表示一个区间，子节点则分别表示父节点的左右半区间，例如父亲的区间是[a,b]，那么(c=(a+b)/2)左儿子的区间是[a,c]，右儿子的区间是[c+1,b]。

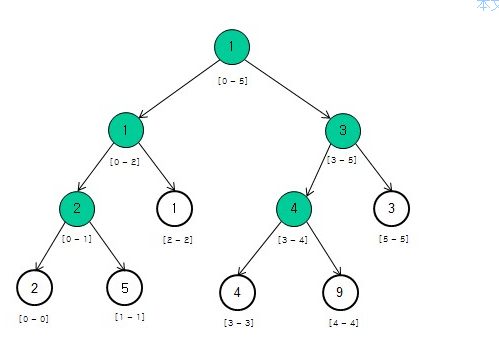
构造线段树示例：

例如对于数组[2, 5, 1, 4, 9, 3]可以构造如下的二叉树（背景为白色表示叶子节点，非叶子节点的值是其对应数组区间内的最小值，例如根节点表示数组区间arr[0...5]内的最小值是1）：

下面请看具体代码：

package com.liuzhen.systemExe;

import java.util.Scanner;

public class Main{

    public int[][] segTree;
    /*
     * 参数root:代表线段树的根节点，此处使用数组存放线段树，其根节点从0开始计数，那么其两个子节点编号必定满足2*root+1或者2*root+2
     * 参数array:给定的目标数组，需要转成相应功能的线段树
     * 参数start:线段树划分给定数组区间的起始位置
     * 参数end:线段树划分给定数组区间的末尾位置
     * 函数功能：返回一个线段树，其所有节点均存放当前数组子区间内的总和以及最大值
     */
    public void buildSegTree(int root, int[] array, int start, int end) {
        if(start == end) {
            segTree[root][0] = array[start];
            segTree[root][1] = array[start];
        } else {
            int mid = (start + end) / 2;
            buildSegTree(2 * root + 1, array, start, mid);      //递归构造左半子树
            buildSegTree(2 * root + 2, array, mid + 1, end);    //递归构造右半子树
            segTree[root][0] = (segTree[2*root+1][0] > segTree[2*root+2][0] ?
                    segTree[2*root+1][0] : segTree[2*root+2][0]);   //回溯求取当前节点区间存放的元素最大值
            segTree[root][1] = segTree[root*2+1][1] + segTree[root*2+2][1]; //回溯求取当前节点区间存放的元素总和
        }
    }
    /*
     * 参数root:开始进行查找的根节点对应的数组下标值
     * 参数start-end:当前节点所表示的区间
     * 参数qstart-qend:此次查询的区间
     * 函数功能：查询当前区间qstart-qend的最大值
     */
    public int querySegTreeMax(int root, int start, int end, int qstart, int qend) {
        if(qstart > end || qend < start)
            return 0;
        int max = 0;
        if(qstart <= start && qend >= end) {
            return segTree[root][0];
        } else {
            int mid = (start + end) / 2;
            int temp1 = querySegTreeMax(root * 2 + 1, start, mid, qstart, qend);
            int temp2 = querySegTreeMax(root * 2 + 2, mid + 1, end, qstart, qend);
            if(temp1 > temp2)
                max = temp1;
            else
                max = temp2;

        }
        return max;
    }
    /*
     * 参数root:开始进行查找的根节点对应的数组下标值
     * 参数start-end:当前节点所表示的区间
     * 参数qstart-qend:此次查询的区间
     * 函数功能：查询当前区间qstart-qend的总和
     */
    public int querySegTreeSum(int root, int start, int end, int qstart, int qend) {
        if(qstart > end || qend < start )
            return 0;
        int sum = 0;
        if(qstart == start && qend == end) {
            return segTree[root][1];
        } else {
            int mid = (start + end) / 2;
            if(qstart <= mid && qend > mid) {
                int temp1 = querySegTreeSum(root * 2 + 1, start, mid, qstart, mid);
                int temp2 = querySegTreeSum(root * 2 + 2, mid + 1, end, mid + 1, qend);
                sum = temp1 + temp2;
            } else if(qstart > mid) {
                int temp2 = querySegTreeSum(root * 2 + 2, mid + 1, end, qstart, qend);
                sum = temp2;
            } else if(qend <= mid) {
                int temp1 = querySegTreeSum(root * 2 + 1, start, mid, qstart, qend);
                sum = temp1;
            }
        }
        return sum;
    }
    /*
     * 参数root:开始进行查找的根节点对应的数组下标值
     * 参数qstart-qend:当前节点所表示的区间
     * 函数功能：把数组下标为index的元素值变成value，并更新线段树
     */
    public void updateSegTree(int root, int qstart, int qend, int index, int value) {
        if(qstart == qend) {
            if(index == qstart) {
                segTree[root][0] = value;
                segTree[root][1] = value;
            }
            return;
        }

        int mid = (qstart + qend) / 2;
        if(mid >= index) {
            updateSegTree(root * 2 + 1, qstart, mid, index, value);
        } else {
            updateSegTree(root * 2 + 2, mid + 1, qend, index, value);
        }
        //回溯更新改变值元素值的根节点相应值
        segTree[root][0] = (segTree[root*2+1][0] > segTree[root*2+2][0] ?
                segTree[root*2+1][0] : segTree[root*2+2][0]);
        segTree[root][1] = segTree[root*2+1][1] + segTree[root*2+2][1];
    }

    public void printResult(int[] A, int[][] operation) {
        segTree = new int[4 * A.length][2];//此处初始化线段树行的长度为4 * n，有n个元素的数组构造的线段树其对应的二叉树层数最大可以达到4*n个节点
        buildSegTree(0, A, 0, A.length - 1);
        for(int i = 0;i < operation.length;i++) {
            if(operation[i][0] == 1) {
                updateSegTree(0, 0, A.length - 1, operation[i][1] - 1, operation[i][2]);
            } else if(operation[i][0] == 2) {
                int sum = querySegTreeSum(0, 0, A.length - 1, operation[i][1] - 1, operation[i][2] - 1);
                System.out.println(sum);
            } else if(operation[i][0] == 3) {
                int max = querySegTreeMax(0, 0, A.length - 1, operation[i][1] - 1, operation[i][2] - 1);
                System.out.println(max);
            }
        }
    }

    public static void main(String[] args){
        Main test = new Main();
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        if(n >100000 || n <= 0 || m > 100000 || m <= 0)   //此处是依据题意给定范围做判断
            return;
        int[] A = new int[n];
        for(int i = 0;i < n;i++)
            A[i] = in.nextInt();
        int[][] operation = new int[m][3];
        for(int i = 0;i < m;i++) {
               for(int j = 0;j < 3;j++) {
                operation[i][j] = in.nextInt();
            }
        }
        test.printResult(A, operation);
    }
}

参考资料：

1.一步一步理解线段树