[BZOJ2946][Poi2000]公共串解题报告|后缀自动机

　　鉴于SAM要简洁一些...于是又写了一遍这题...

　　不过很好呢又学到了一些新的东西...

　　这里是用SA做这道题的方法

　　首先还是和两个字符串的一样，为第一个字符串建SAM

　　然后每一个字符串再在这个SAM上跑匹配

　　然而我们最后要的答案是什么呢？

　　是某个在所有字符串中匹配长度最小值最大的状态子串

　　然后对于每一个字符串

　　我们可以记录它在每一个状态子串上的最大匹配长度

　　最后需要一个非常关键的转移

　　就是用当前节点的值更新fail指针指向的节点

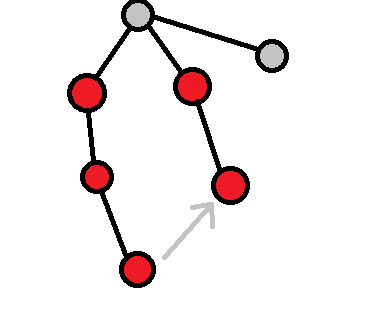
　　比如这种情况

　　如果一次匹配到左边的三个节点，一次匹配到右边的两个节点（两次匹配在不同的字符串中）

　　那么显然，这两个字符串的公共子串长度为2是存在的

　　但是由于我们没有转移过，fail指针指向的点没有储存前面的信息就会出错

　　

　　然后至于转移的顺序，我们可以按照深度顺序

　　这个可以用桶排实现

 program bzoj2946;
 const maxn = ;
 var n,i,j,now,maxl,root,c,tot,cnt,t:longint;
     s:array[..]of ansistring;
     mx,fail,q,b,ans,tem:array[-..maxn]of longint;
     a:array[-..maxn,-..]of longint;

 function max(a,b:longint):longint;
 begin
     if a>b then exit(a) else exit(b);
 end;

 function min(a,b:longint):longint;
 begin
     if a<b then exit(a) else exit(b);
 end;

 function insert(p,c:longint):longint;
 var np,q,nq:longint;
 begin
     inc(cnt);np:=cnt;mx[np]:=mx[p]+;
     while (p<>)and(a[p,c]=) do
     begin
         a[p,c]:=np;p:=fail[p];
     end;
     if p= then fail[np]:=root else
     begin
         q:=a[p,c];
         if mx[q]=mx[p]+ then fail[np]:=q else
         begin
             inc(cnt);nq:=cnt;mx[nq]:=mx[p]+;
             a[nq]:=a[q];
             fail[nq]:=fail[q];
             fail[np]:=nq;fail[q]:=nq;
             while a[p,c]=q do
             begin
                 a[p,c]:=nq;p:=fail[p];
             end;
         end;
     end;
     exit(np);
 end;

 begin
     readln(n);
     for i:= to n do readln(s[i]);
     cnt:=;root:=;t:=root;
     for i:= to length(s[]) do t:=insert(t,ord(s[,i])-);
     for i:= to cnt do ans[i]:=mx[i];
     fillchar(b,sizeof(b),);
     for i:= to cnt do inc(b[mx[i]]);
     for i:= to cnt do inc(b[i],b[i-]);
     for i:= to cnt do ans[i]:=mx[i];
     for i:=cnt downto  do
     begin
         dec(b[mx[i]]);
         q[b[mx[i]]]:=i;
     end;
     for i:= to n do
     begin
         now:=root;maxl:=;
         fillchar(tem,sizeof(tem),);
         for j:= to length(s[i]) do
         begin
             c:=ord(s[i][j])-;
             if a[now,c]<> then begin now:=a[now,c];inc(maxl);end else
             begin
                 while (now<>)and(a[now,c]=) do now:=fail[now];
                 if now= then begin now:=root;maxl:=;end else begin maxl:=mx[now]+;now:=a[now,c];end;
             end;
             tem[now]:=max(tem[now],maxl);
         end;
         for j:=cnt downto  do tem[fail[q[j]]]:=max(tem[fail[q[j]]],tem[q[j]]);
         for j:= to cnt do ans[j]:=min(ans[j],tem[j]);
     end;
     tot:=;
     for i:= to cnt do if ans[i]>tot then tot:=ans[i];
     writeln(tot);
 end.

　　比较了一下..代码减少了三分之一，空间缩小了十分之九...最主要写起来简单多了

　　SAM大法好

　　

　　05/.May