LightOJ 1375 - LCM Extreme 莫比乌斯反演或欧拉扩展

**题意:**给出n [1,3*1e6] 求
并模2^64。
**思路:**先手写出算式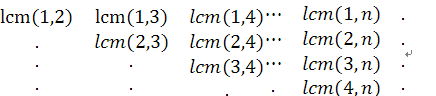

观察发现可以化成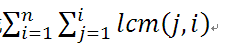

那么关键在于如何求得i为1~n的lcm(i,n)之和。可以知道lcm(a,b)为ab/gcd(a,b)

变换得(a/gcd) * (b/gcd)gcd 由于GCD的性质，可以知道a/gcd 与 b/gcd是互质的两个质数。由此可以想到应用欧拉函数，并且由性质能够证明 n*phi(n)/2为小于n所有与n互质数之和（证明:已知一个质数p那么显然n-p与它互质，那么phi(n)中有phi(n)/2对数，每对数和为n）

故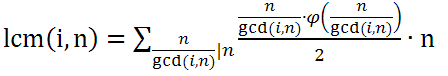

设n/gcd(I,n)为d则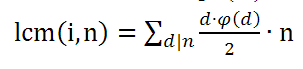

由此题目化成枚举d即可。还需注意格式的控制转换，本题需要模2^64 只需设unsigned long long 溢出即模，内存限制是刚好卡住的。

#include <stdio.h>

#include <iostream>

#include <string.h>

#include <algorithm>

#include <utility>

#include <vector>

#include <map>

#include <set>

#include <string>

#include <stack>

#include <queue>

#define LL unsigned long long

#define MMF(x) memset((x),0,sizeof(x))

#define MMI(x) memset((x), INF, sizeof(x))

using namespace std;



const int INF = 0x3f3f3f3f;

const int N = 1e6+10;



int eul[3*N];

LL fa[3*N];

LL ans[3*N];

void eular()

{

    MMF(eul);

    MMF(fa);



    eul[1] = 1;

    for(int i = 2; i < 3*N; i++)

    {

        if(!eul[i])

        {

            for(int j = i; j < 3*N; j+=i)

            {

                if(!eul[j])

                    eul[j] = j;

                eul[j] = eul[j]/i * (i-1);

            }

        }

    }

    ans[0] = ans[1] = 0;

    for(LL i = 2; i < 3*N; i++)

    {

        for(LL j = i; j < 3*N; j += i)

        {

            LL t =  j * eul[i] / 2;

            fa[j] += i* t;

        }

        ans[i] = ans[i-1] + fa[i];

    }

}



int main()

{

    eular();

    int T;

    int cnt = 0;

    scanf("%d", &T);

    while(T--)

    {

        LL n;

        scanf("%llu", &n);

        printf("Case %d: %llu\n", ++cnt, ans[n]);

        //printf("%d\n",eul[3000000]);

    }

    return 0;

}

/*

5

2

10

13

100000

3000000

**/