Codeforces Round #448(Div.2) Editorial ABC

被B的0的情况从头卡到尾。导致没看C,心情炸裂又掉分了。

A. Pizza Separation

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Students Vasya and Petya are studying at the BSU (Byteland State University). At one of the breaks they decided to order a pizza. In this problem pizza is a circle of some radius. The pizza was delivered already cut into n pieces. The i-th piece is a sector of angle equal to ai. Vasya and Petya want to divide all pieces of pizza into two continuous sectors in such way that the difference between angles of these sectors is minimal. Sector angle is sum of angles of all pieces in it. Pay attention, that one of sectors can be empty.

Input

The first line contains one integer n (1 ≤ n ≤ 360)  — the number of pieces into which the delivered pizza was cut.

The second line contains n integers ai (1 ≤ ai ≤ 360)  — the angles of the sectors into which the pizza was cut. The sum of all ai is 360.

Output

Print one integer  — the minimal difference between angles of sectors that will go to Vasya and Petya.

Examples

input

4
90 90 90 90

output

0

input

3
100 100 160

output

40

input

1
360

output

360

input

4
170 30 150 10

output

0

Note

In first sample Vasya can take 1 and 2 pieces, Petya can take 3 and 4 pieces. Then the answer is |(90 + 90) - (90 + 90)| = 0.

In third sample there is only one piece of pizza that can be taken by only one from Vasya and Petya. So the answer is |360 - 0| = 360.

In fourth sample Vasya can take 1 and 4 pieces, then Petya will take 2 and 3 pieces. So the answer is |(170 + 10) - (30 + 150)| = 0.

Picture explaning fourth sample:

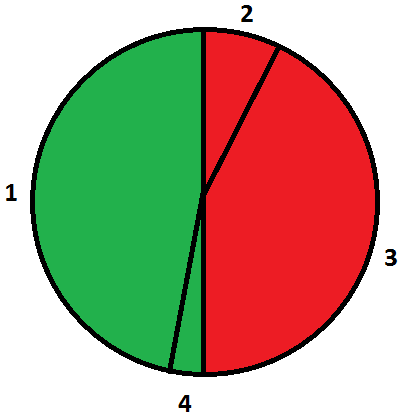
Both red and green sectors consist of two adjacent pieces of pizza. So Vasya can take green sector, then Petya will take red sector.

---

 

题意：

给你一块按半径分成n块的披萨，并按顺序（顺时针或逆时针）给出这n块的角度，现在你要把其中连续k块合成一块，剩下的合成一块，求最小的角度之差，允许角度为0的块出现。

题解：

O（n^2）以每块披萨为起始找一下就好了。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define LL long long
 #define mod 1000000007
 #define INF 0x3f3f3f3f
 using namespace std;
 const int N=;
 int a[N],n,m,all,mindif;
 set<int> num,num2;
 set<int>::iterator it;
 int main()
 {
     scanf("%d",&n);
     all=;
     mindif=INF;
     for(int i=;i<=n;i++)
     {
         scanf("%d",&a[i]);
     }
     for(int i=;i<=n;i++)
     {
         all=;
         for(int j=i;j<=i+n;j++)
         {
             all+=a[(j-)%n+];
             if(abs(-*all)<mindif)
                 mindif=abs(-*all);
         }
     }
     printf("%d\n",mindif);
     return ;
 }

B. XK Segments

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

While Vasya finished eating his piece of pizza, the lesson has already started. For being late for the lesson, the teacher suggested Vasya to solve one interesting problem. Vasya has an array a and integer x. He should find the number of different ordered pairs of indexes(i, j) such that ai ≤ aj and there are exactly k integers y such that ai ≤ y ≤ aj and y is divisible by x.

In this problem it is meant that pair (i, j) is equal to (j, i) only if i is equal to j. For example pair (1, 2) is not the same as (2, 1).

Input

The first line contains 3 integers n, x, k (1 ≤ n ≤ 105, 1 ≤ x ≤ 109, 0 ≤ k ≤ 109), where n is the size of the array a and x and k are numbers from the statement.

The second line contains n integers ai (1 ≤ ai ≤ 109) — the elements of the array a.

Output

Print one integer — the answer to the problem.

Examples

input

4 2 1
1 3 5 7

output

3

input

4 2 0
5 3 1 7

output

4

input

5 3 1
3 3 3 3 3

output

25

Note

In first sample there are only three suitable pairs of indexes — (1, 2), (2, 3), (3, 4).

In second sample there are four suitable pairs of indexes(1, 1), (2, 2), (3, 3), (4, 4).

In third sample every pair (i, j) is suitable, so the answer is 5 * 5 = 25.

---

题意：

给你长度为n的数列a，然后让你找出所有的对（i,j）满足a_i≤a_j并且[a_i，a_j]中能整除X的数有且仅能有k个，问这样的对数总数。其中(i,j) 与(j,i),i≠j视为不同对，(i,i)与(i,i)为同一对。

题解：

把左右区间端点分开，那么[l,r]整除x的数的数量为r/x-(l-1)/x。读入的时候把他们（r/x 和(l-1)/x）加入对应的map  l和r 中，然后用迭代器it遍历r的map，找对应的 l 中 it->first -k 的数量乘上it->second的数量加入答案中即可。

然后要特判下0的情况，0的话把所有数都加入一个map中，然后遍历这个map，对于每个map对，把他的it->second乘上它前面first/x值为it->first/x的对的个数为答案的贡献。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define LL long long
 #define mod 1000000007
 #define INF 0x3f3f3f3f
 using namespace std;
 const int N=1e5+;
 map<LL,LL> r,l,a;
 map<LL,LL>::iterator it;
 LL x,k;
 int n,m,p;
 LL ans,num;
 int main()
 {
     scanf("%d%I64d%I64d",&n,&x,&k);
     for(int i=;i<=n;i++)
     {
         scanf("%I64d",&num);
         l[(num-)/x]++;
         r[num/x]++;
         a[num]++;
     }
     ans=;
     if(k==)
     {
         p=;
         k=;
         m=;
         for(it=a.begin();it!=a.end();it++)
         {
             m+=(int)it->second;
             if( it->first/x > k)
             {
                 p=m;
                 if( it->first % x !=)
                     p-=(int)it->second;
             }
             k=it->first/x;
             ans+=(LL)(m-p) * it->second;
         }
         printf("%I64d\n",ans);
         return ;
     }
     for(it=r.begin();it!=r.end();it++)
         ans+=l[it->first-k]*it->second;
     printf("%I64d\n",ans);
     return ;
 }

C. Square Subsets

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Petya was late for the lesson too. The teacher gave him an additional task. For some array a Petya should find the number of different ways to select non-empty subset of elements from it in such a way that their product is equal to a square of some integer.

Two ways are considered different if sets of indexes of elements chosen by these ways are different.

Since the answer can be very large, you should find the answer modulo 109 + 7.

Input

First line contains one integer n (1 ≤ n ≤ 105) — the number of elements in the array.

Second line contains n integers ai (1 ≤ ai ≤ 70) — the elements of the array.

Output

Print one integer — the number of different ways to choose some elements so that their product is a square of a certain integer modulo109 + 7.

Examples

input

4
1 1 1 1

output

15

input

4
2 2 2 2

output

7

input

5
1 2 4 5 8

output

7

Note

In first sample product of elements chosen by any way is 1 and 1 = 12. So the answer is 24 - 1 = 15.

In second sample there are six different ways to choose elements so that their product is 4, and only one way so that their product is 16. So the answer is 6 + 1 = 7.

---

题意：

给你n个≤70的数，问有几种取数方式能使取出来的数乘积为完全平方数。

题解：

考虑70内的质因子只有19个。那么每个数字都能表示为19维的01向量，每一维表示该位质因子在该数出现的幂次的奇偶。1为奇0为偶。把他转换为一个二进制数。

那么数的乘积为完全平方数就相当于取这n个19维的01向量的一个组合，使得xor结果为0。

那么写个最高19位的线性基，然后看看线性基里大于0的数的个数lct。答案即为$ 2^{n-lct}-1 $，这是线性基中组合出现相同数的一个结论。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define LL long long
 #define INF 0x3f3f3f3f
 using namespace std;
 const int N=1e5+;
 const int M=1e2+;
 const LL mod=1e9+;
 int prime[M],inf[M],pcnt,n,m,k,p,t;
 int liner[],lcnt;
 LL quick_pow(LL x,LL n)
 {
     LL res=;
     x%=mod;
     while(n)
     {
         if(n&)
             res=(res*x)%mod;
         n>>=;
         x=(x*x)%mod;
     }
     return res;
 }
 void init()
 {
     clr(inf);
     pcnt=;
     lcnt=;
     for(int i=;i<=;i++)
     {
         if(!inf[i])
         {
             prime[++pcnt]=i;
             inf[i]=;
         }
         for(int j=;j<=pcnt;j++)
         {
             if(i>/prime[j]) break;
             inf[prime[j]*i]=;
             if(i%prime[j]==) break;
         }
     }
     clr(liner);
     return ;
 }
 int main()
 {
     init();
     scanf("%d",&n);
     for(int i=;i<=n;i++)
     {
         scanf("%d",&p);
         k=;
         for(int j=;j<=pcnt;j++)
         {
             k<<=;
             while(!(p%prime[j]))
             {
                 k^=;
                 p/=prime[j];
             }
         }
         for(int j=pcnt;j>=;j--)
         {
             if(k>>j)
             {
                 if(liner[j]) k^=liner[j];
                 else
                 {
                     liner[j]=k;
                     break;
                 }
             }
         }
     }
     for(int i=pcnt;i>=;i--)
         if(liner[i])
         {
             lcnt++;
         }
     printf("%lld\n",(quick_pow(,(LL)(n-lcnt))-+mod)%mod);
     return ;
 }