cf509E Pretty Song

E. Pretty Song

time limit per test 1 second

memory limit per test 256 megabytes

input standard input

output standard output

When Sasha was studying in the seventh grade, he started listening to music a lot. In order to evaluate which songs he likes more, he introduced the notion of the song's prettiness. The title of the song is a word consisting of uppercase Latin letters. The prettiness of the song is the prettiness of its title.

Let's define the simple prettiness of a word as the ratio of the number of vowels in the word to the number of all letters in the word.

Let's define the prettiness of a word as the sum of simple prettiness of all the substrings of the word.

More formally, let's define the function vowel(c) which is equal to 1, if c is a vowel, and to 0 otherwise. Let si be the i-th character of strings, and si..j be the substring of word s, staring at the i-th character and ending at the j-th character (sisi + 1... sj, i ≤ j).

Then the simple prettiness of s is defined by the formula:

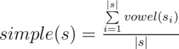
The prettiness of s equals

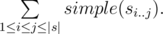
Find the prettiness of the given song title.

We assume that the vowels are I, E, A, O, U, Y.

Input

The input contains a single string s (1 ≤ |s| ≤ 5·105) — the title of the song.

Output

Print the prettiness of the song with the absolute or relative error of at most 10 - 6.

Sample test(s)

input

IEAIAIO

output

28.0000000

input

BYOB

output

5.8333333

input

YISVOWEL

output

17.0500000

Note

In the first sample all letters are vowels. The simple prettiness of each substring is 1. The word of length 7 has 28 substrings. So, theprettiness of the song equals to 28.

题意是把字符串变成01串，元音字母是1其他是0，然后一个子串[l,r]对答案的贡献是(s[r]-s[l-1])/(r-l+1)，求答案

枚举分母k，那么答案就是Σ(s[k]-s[0]+s[k+1]-s[1]+...+s[n]-s[n-k+1])/k

令t[]是s的前缀和，那么答案就是Σ(t[n]-t[n-k+1]-t[k])/k

O(n)搞定了

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<ctime>
#define LL long long
#define inf 0x7fffffff
#define pa pair<int,int>
#define pi 3.1415926535897932384626433832795028841971
using namespace std;
inline LL read()
{
    LL x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n;
char ch[1000010];
int a[1000010];
LL s[1000010],t[1000010];
double ans;
int main()
{
	scanf("%s",ch+1);
	n=strlen(ch+1);
	for(int i=1;i<=n;i++)
		a[i]=ch[i]=='A'||ch[i]=='E'||ch[i]=='I'||ch[i]=='O'||ch[i]=='U'||ch[i]=='Y';
	for(int i=1;i<=n;i++)
	{
		s[i]=s[i-1]+a[i];
		t[i]=t[i-1]+s[i];
	}
	for(int i=1;i<=n;i++)
	{
		ans+=(double)(t[n]-t[i-1]-t[n-i])/(i+0.0);
	}
	printf("%.6lf\n",ans);
}