hdu6440 Dream 2018CCPC网络赛C 费马小定理+构造

题目传送门

题目大意：

给定一个素数p，让你重载加法运算和乘法运算，使（m+n）^p=m^p+n^p，并且

存在一个小于p的q，使集合{q^k|0<k<p,k∈Z} 等于集合{k|0<k<p,k∈Z}.

然后输出两个矩阵，第一个矩阵输出i+j的值，第二个矩阵输出i*j的值。（题意好难懂，你们怎么都看懂了！！）

思路：

由费马小定理得到，当p是质数的时候，a^p-1 ≡ 1（mod p），两边同乘以a，也就是说当a^p和a在取模p的时候相等

所以（m+n）^p=m+n=m^p+n^p（乘法为x*x%p）。那么将x*y定义成x*y%p，就可以满足这一条件。

而此时第二个约束条件就是原根的性质了。

若g是模p的原根，则 gⁱmod p  的值两两不相同，且，1<g<p , 0<i<p.

而加法就可以随便定义了，只要不和上面的条件冲突（应该是这样），我定义的是 x+y=x。（注意，此时的+已经是一种新的符号了，不能和减法互推，y此时不等于0）。

定理：设是正整数，是整数，若模的阶等于，则称为模的一个原根。

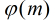
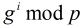
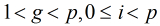
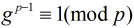
假设一个数对于模来说是原根，那么的结果两两不同,且有，那么可以称为是模的一个原根，归根到底就是当且仅当指数为的时候成立。（这里是素数）

模有原根的充要条件：，其中是奇素数。

原根博客

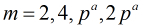
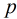
 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #define CLR(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 typedef long long ll;
 ll p;
 inline ll mul(ll x, ll y) {
     return x * y % p;
 }
 int main() {
     int T;
     cin >> T;
     while (T--) {
         scanf("%lld", &p);
         for (int i = ; i < p; i++) {
             for (int j = ; j < p; j++) {
                 printf("%d%c", i, (j == p - ) ? '\n' : ' ');
             }
         }
         for (int i = ; i < p; i++) {
             for (int j = ; j < p; j++) {
                 printf("%lld%c", mul(i, j), (j == p - ) ? '\n' : ' ');
             }
         }
     }

 }

Dream

Time Limit: 12000/6000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1210    Accepted Submission(s): 357
Special Judge

Problem Description

Freshmen frequently make an error in computing the power of a sum of real numbers, which usually origins from an incorrect equation (m+n)p=mp+np, where m,n,p are real numbers. Let's call it ``Beginner's Dream''.

For instance, (1+4)2=52=25, but 12+42=17≠25. Moreover, 9+16−−−−−√=25−−√=5, which does not equal 3+4=7.

Fortunately, in some cases when p is a prime, the identity

(m+n)p=mp+np

holds true for every pair of non-negative integers m,n which are less than p, with appropriate definitions of addition and multiplication.

You are required to redefine the rules of addition and multiplication so as to make the beginner's dream realized.

Specifically, you need to create your custom addition and multiplication, so that when making calculation with your rules the equation (m+n)p=mp+np is a valid identity for all non-negative integers m,n less than p. Power is defined as

ap={1,ap−1⋅a,p=0p>0

Obviously there exists an extremely simple solution that makes all operation just produce zero. So an extra constraint should be satisfied that there exists an integer q(0<q<p) to make the set {qk|0<k<p,k∈Z} equal to {k|0<k<p,k∈Z}. What's more, the set of non-negative integers less than p ought to be closed under the operation of your definitions.

Hint

Hint for sample input and output:
From the table we get 0+1=1, and thus (0+1)2=12=1⋅1=1. On the other hand, 02=0⋅0=0, 12=1⋅1=1, 02+12=0+1=1.
They are the same.

 

Input

The first line of the input contains an positive integer T(T≤30) indicating the number of test cases.

For every case, there is only one line contains an integer p(p<210), described in the problem description above. p is guranteed to be a prime.

 

Output

For each test case, you should print 2p lines of p integers.

The j-th(1≤j≤p) integer of i-th(1≤i≤p) line denotes the value of (i−1)+(j−1). The j-th(1≤j≤p) integer of (p+i)-th(1≤i≤p) line denotes the value of (i−1)⋅(j−1).

 

Sample Input

1
2

 

Sample Output

0 1
1 0
0 0
0 1