【NOIP 2009】最优贸易

描述

C 国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。任意两个
城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路，一部分
为双向通行的道路，双向通行的道路在统计条数时也计为 1 条。 
C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价
格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。 
商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息
之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 C 国 n 个城
市的标号从 1~ n，阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。在旅游的
过程中，任何城市可以重复经过多次，但不要求经过所有 n 个城市。阿龙通过这样的贸易方
式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另
一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游，他决定
这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。 
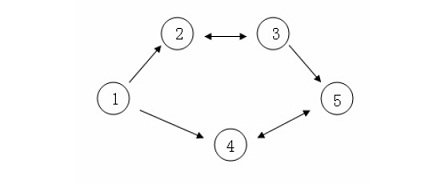
假设 C 国有 5 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路
为单向通行，双向箭头表示这条道路为双向通行。

假设 1~n 号城市的水晶球价格分别为 4，3，5，6，1。 
阿龙可以选择如下一条线路：1->2->3->5，并在 2 号城市以 3 的价格买入水晶球，在 3
号城市以 5的价格卖出水晶球，赚取的旅费数为 2。 
阿龙也可以选择如下一条线路 1->4->5->4->5，并在第 1 次到达 5 号城市时以 1 的价格
买入水晶球，在第 2 次到达 4 号城市时以 6 的价格卖出水晶球，赚取的旅费数为 5。

现在给出 n个城市的水晶球价格，m条道路的信息（每条道路所连接的两个城市的编号
以及该条道路的通行情况） 。请你告诉阿龙，他最多能赚取多少旅费。

格式

输入格式

第一行包含 2 个正整数 n 和 m，中间用一个空格隔开，分别表示城市的数目和道路的
数目。 
第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城
市的商品价格。 
接下来 m行， 每行有 3 个正整数， x， y， z， 每两个整数之间用一个空格隔开。 如果 z=1，
表示这条道路是城市 x到城市 y之间的单向道路；如果 z=2，表示这条道路为城市 x 和城市
y之间的双向道路。

输出格式

输出共1 行， 包含 1 个整数， 表示最多能赚取的旅费。 如果没有进行贸易，
则输出 0。

样例1

样例输入1

5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2 

样例输出1

5

限制

每个测试点1s

输入数据保证 1 号城市可以到达n 号城市。
对于 10%的数据，1≤n≤6。
对于 30%的数据，1≤n≤100。
对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。
对于 100%的数据，1≤n≤100000，1≤m≤500000，1≤x，y≤n，1≤z≤2，1≤各城市
水晶球价格≤100。

题解

此题好多人都用最短路写的，但我觉得用搜索就足以了（虽然本质差不多）。

建图：

此题需要建一个正向图（e1）和一个反向图（e2）；

下面讲解为什么。

BFS：

正向图从1点开始搜并更新buy[]（取min），反向图从n点开始搜sell[]（取max）；

从n点跑反向图是因为此题要求一定要先买后卖；

buy[i]表示到i点最小买入；sell[i]表示到i点最大卖出；

queue<int> q;
void bfs1(int u){
    memset(buy,0x3f,sizeof(buy));
    memset(vis,,sizeof(vis));
    q.push(u);
    while(!q.empty()){
        int x=q.front();q.pop();
        if(vis[x])continue;vis[x]=;
        for(int i=h1[x];i;i=e1[i].nex){
            int xx=e1[i].to;
            buy[xx]=min(a[xx],buy[x]);
            q.push(xx);
        }
    }
}
void bfs2(int u){
    memset(sell,-0x3f,sizeof(sell));
    memset(vis,,sizeof(vis));
    q.push(u);
    while(!q.empty()){
        int x=q.front();q.pop();
        if(vis[x])continue;vis[x]=;
        for(int i=h2[x];i;i=e2[i].nex){
            int xx=e2[i].to;
            sell[xx]=max(a[xx],sell[x]);
            q.push(xx);
        }
    }
}

code：

代码应该不算长

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cctype>
 #include<queue>
 #define ll long long
 using namespace std;
 const int N=;
 int read()
 {
     int X=,w=; char ch=;
     while(!isdigit(ch)) {w|=ch=='-';ch=getchar();}
     while(isdigit(ch)) X=(X<<)+(X<<)+(ch^),ch=getchar();
     return w?-X:X;
 }
 int n,m,a[N],h1[N],h2[N],ans,tot,buy[N],sell[N];
 bool vis[N];
 struct node{
     int nex,to;
 }e1[N],e2[N];
 void add(int u,int v){
     e1[++tot].nex=h1[u];
     e1[tot].to=v;
     h1[u]=tot;
     e2[tot].nex=h2[v];
     e2[tot].to=u;
     h2[v]=tot;
 }
 queue<int> q;
 void bfs1(int u){
     memset(buy,0x3f,sizeof(buy));
     memset(vis,,sizeof(vis));
     q.push(u);
     while(!q.empty()){
         int x=q.front();q.pop();
         if(vis[x])continue;vis[x]=;
         for(int i=h1[x];i;i=e1[i].nex){
             int xx=e1[i].to;
             buy[xx]=min(a[xx],buy[x]);
             q.push(xx);
         }
     }
 }
 void bfs2(int u){
     memset(sell,-0x3f,sizeof(sell));
     memset(vis,,sizeof(vis));
     q.push(u);
     while(!q.empty()){
         int x=q.front();q.pop();
         if(vis[x])continue;vis[x]=;
         for(int i=h2[x];i;i=e2[i].nex){
             int xx=e2[i].to;
             sell[xx]=max(a[xx],sell[x]);
             q.push(xx);
         }
     }
 }
 signed main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)a[i]=read();
     for(int i=;i<=m;i++){
         int x,y,z;
         x=read();y=read();z=read();
         if(z==)add(x,y);
         if(z==)add(x,y),add(y,x);
     }
     bfs1();
     bfs2(n);
     for(int i=;i<=n;i++)
         ans=max(sell[i]-buy[i],ans);
     printf("%d",ans);
     return ;
 }

-^-^--ZAGER--^-^-