[TJOI2013]循环格费用流 BZOJ3171

题目背景

一个循环格就是一个矩阵,其中所有元素为箭头,指向相邻四个格子。每个元素有一个坐标(行,列),其中左上角元素坐标为(0,0)。给定一个起始位(r,c),你可以沿着箭头方向在格子间行走。即:如果(r,c)是一个左箭头，那么走到(r,c-1);如果是一个右箭头,走到(r,c+1);如果是上箭头,走到(r-1,c);如果是下箭头,走到(r+1,c)。每一行和每一列都是循环的,即如果走出边界,你会出现在另一侧。比如在一个5*5的循环格里,从(3,0)向左走会出现在(3,4)。

题目描述

一个完美的循环格是这样定义的:对于任意一个起始位置,你都可以沿着箭头最终回到起始位置。如果一个循环格不满足完美,你可以随意修改任意一个元素的箭头直到完美。例如下图,左边不是一个完美的循环格,因为只有从(1,1),(1,2),(2,0),(2,3)出发才会回到起始位置。通过修改其中两个箭头,可以得到右图,一个完美的循环格。

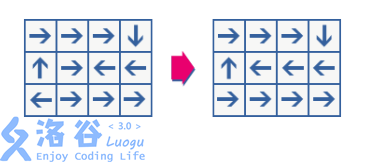
给定一个循环格,你需要计算最少需要修改多少个元素使其完美。

输入输出格式

输入格式：

第一行两个整数R和C,表示循环格的行和列。接下来R行,每一行包含C个字符LRUD表示左右上下

输出格式：

一个整数,表示最少需要修改多少个元素使得给定的循环格完美。

输入输出样例

输入样例#1：
复制

4 4

RRRD

URDD

UULD

ULLL

输出样例#1： 复制

输入样例#2： 复制

3 4

RRRD

URLL

LRRR

输出样例#2： 复制

说明

数据范围

30%的数据，1 ≤ R, C ≤ 7

100%的数据，1 ≤ R, C ≤ 15

我的代码貌似常数比较大。。

#include<iostream>

#include<cstdio>

#include<algorithm>

#include<cstdlib>

#include<cstring>

#include<string>

#include<cmath>

#include<map>

#include<set>

#include<vector>

#include<queue>

#include<bitset>

#include<ctime>

#include<deque>

#include<stack>

#include<functional>

#include<sstream>

//#include<cctype>

//#pragma GCC optimize(2)

using namespace std;

#define maxn 1000005

#define inf 0x7fffffff

//#define INF 1e18

#define rdint(x) scanf("%d",&x)

#define rdllt(x) scanf("%lld",&x)

#define rdult(x) scanf("%lu",&x)

#define rdlf(x) scanf("%lf",&x)

#define rdstr(x) scanf("%s",x)

typedef long long  ll;

typedef unsigned long long ull;

typedef unsigned int U;

#define ms(x) memset((x),0,sizeof(x))

const long long int mod = 1e9 + 7;

#define Mod 1000000000

#define sq(x) (x)*(x)

#define eps 1e-4

typedef pair<int, int> pii;

#define pi acos(-1.0)

//const int N = 1005;

#define REP(i,n) for(int i=0;i<(n);i++)

typedef pair<int, int> pii;

inline ll rd() {

	ll x = 0;

	char c = getchar();

	bool f = false;

	while (!isdigit(c)) {

		if (c == '-') f = true;

		c = getchar();

	}

	while (isdigit(c)) {

		x = (x << 1) + (x << 3) + (c ^ 48);

		c = getchar();

	}

	return f ? -x : x;

}

ll gcd(ll a, ll b) {

	return b == 0 ? a : gcd(b, a%b);

}

int sqr(int x) { return x * x; }

/*ll ans;

ll exgcd(ll a, ll b, ll &x, ll &y) {

	if (!b) {

		x = 1; y = 0; return a;

	}

	ans = exgcd(b, a%b, x, y);

	ll t = x; x = y; y = t - a / b * y;

	return ans;

}

*/

bool vis[maxn];

int n, m, s, t;

int x, y, f, z;

int dis[maxn], pre[maxn], last[maxn], flow[maxn];

int maxflow, mincost;

struct node {

	int to, nxt, flow, dis;

}edge[maxn << 2];

int head[maxn], cnt;

queue<int>q;

void addedge(int from, int to, int flow, int dis) {

	edge[++cnt].to = to; edge[cnt].flow = flow; edge[cnt].dis = dis;

	edge[cnt].nxt = head[from]; head[from] = cnt;

}

bool spfa(int s, int t) {

	memset(dis, 0x7f, sizeof(dis)); memset(flow, 0x7f, sizeof(flow));

	ms(vis);

	q.push(s); vis[s] = 1; dis[s] = 0; pre[t] = -1;

	while (!q.empty()) {

		int now = q.front(); q.pop(); vis[now] = 0;

		for (int i = head[now]; i != -1; i = edge[i].nxt) {

			if (edge[i].flow > 0 && dis[edge[i].to] > dis[now] + edge[i].dis) {

				dis[edge[i].to] = edge[i].dis + dis[now];

				pre[edge[i].to] = now; last[edge[i].to] = i;

				flow[edge[i].to] = min(flow[now], edge[i].flow);

				if (!vis[edge[i].to]) {

					vis[edge[i].to] = 1; q.push(edge[i].to);

				}

			}

		}

	}

	return pre[t] != -1;

}

void mincost_maxflow() {

	while (spfa(s, t)) {

		int now = t;

		maxflow += flow[t]; mincost += flow[t] * dis[t];

		while (now != s) {

			edge[last[now]].flow -= flow[t];

			edge[last[now] ^ 1].flow += flow[t];

			now = pre[now];

		}

	}

}

char ch[300][300];

char opt[] = { '0','D','U','L','R' };

int dx[] = { 0,1,-1,0,0 };

int dy[] = { 0,0,0,-1,1 };

int getpos(int x, int y) {

	return (x - 1)*m + y;

}

bool OK(int i, int j) {

	if (i <= n && i >= 1 && j <= m && j >= 1)return true;

	return false;

}

int main() {

	//ios::sync_with_stdio(0);

	memset(head, -1, sizeof(head)); cnt = 1;

	rdint(n); rdint(m);

	for (int i = 1; i <= n; i++)scanf("%s", ch[i] + 1);

	s = 1000; t = s + 1;

	int dt = n * m;

	for (int i = 1; i <= dt; i++) {

		addedge(s, i, 1, 0); addedge(i, s, 0, 0);

	}

	for (int i = 1; i <= dt; i++) {

		addedge(i + dt, t, 1, 0); addedge(t, dt + i, 0, 0);

	}

	for (int i = 1; i <= n; i++) {

		for (int j = 1; j <= m; j++) {

			char tmp = ch[i][j];

			for (int k = 1; k <= 4; k++) {

				int xx = (i + dx[k] + n - 1) % n + 1;

				int yy = (j + dy[k] + m - 1) % m + 1;

				int fg = (tmp == opt[k]) ^ 1;

				addedge(getpos(i, j), getpos(xx, yy) + dt, 1, fg);

				addedge(getpos(xx, yy) + dt, getpos(i, j), 0, -fg);

			}

		}

	}

	mincost_maxflow();

	cout << mincost << endl;

	return 0;

}