Posters TopCoder - 1684

传送门

分析

首先我们不难想到1e4^5的暴力枚举，但显然这是不行的，于是我们考虑对于每一张海报肯定有一种最优情况使得它至少有一条边要么靠着板子的边要么靠着之前的某一张海报的边，这样我们便可以将复杂度优化了很多。我们再考虑将每一种情况进行哈希，这样便可以避免了如图一的情况(矩形中的数字是指这个矩形是第几个被添加进来的)

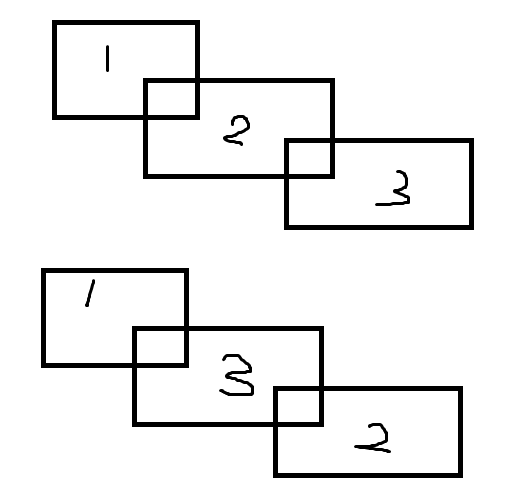图一

我们看得出来这两种实际是一种情况，所以通过哈希我们可以避免重复搜索。在有了这些之后我们再在程序中加一些其它剪枝，用容斥统计答案就行了，详见代码。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<ctime>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
#define sp cout<<"---------------------------------------------------"<<endl
#define uli long long
const uli HASH=;
int n,m,k,a[],b[],x[],y[],ans;
set<uli>vis;
uli gethash(int msk){
    uli hsh=;
    for(int i=;i<k;i++)
    if(msk&(<<i)){
          hsh=hsh*HASH+(uli)x[i]-(uli)x[];
          hsh=hsh*HASH+(uli)y[i]-(uli)y[];
    }else {
          hsh=hsh*HASH+(uli)n;
          hsh=hsh*HASH+(uli)m;
    }
    return hsh;
}
int getans(int msk){
    int i,j,res=;
    for(i=msk;i>;i=(i-)&msk){
    int x1=-,y1=-,x2=n,y2=m;
    for(j=;j<k;j++)
      if(i&(<<j)){
          x1=max(x1,x[j]),y1=max(y1,y[j]);
          x2=min(x2,x[j]+a[j]-);
          y2=min(y2,y[j]+b[j]-);
      }
      if(__builtin_popcount(i)&){
          res+=max(x2-x1+,)*max(y2-y1+,);
      }else res-=max(x2-x1+,)*max(y2-y1+,);
    }
    return res;
}
void fx(int);
void work(int msk,int wh,int xx,int yy){
    if(yy<||yy+b[wh]>m||xx<||xx+a[wh]>n)return;
    x[wh]=xx;y[wh]=yy;
    int res=getans(msk|(<<wh));
    ans=max(ans,res);
    for(int i=;i<k;i++)
    if(i!=wh&&!(msk&(<<i)))
        res+=a[i]*b[i];
    if(res<=ans)return;
    uli hsh=gethash(msk|(<<wh));
    if(vis.find(hsh)==vis.end()){
        vis.insert(hsh);
        fx(msk|(<<wh));
    }
}
void fy(int msk,int wh,int xx){
    int i;
    if(xx<||xx+a[wh]>n)return;
    work(msk,wh,xx,);
    work(msk,wh,xx,m-b[wh]);
    for(i=;i<k;i++)
      if(msk&(<<i)){
          work(msk,wh,xx,y[i]+b[i]);
          work(msk,wh,xx,y[i]-b[wh]);
      }
    }
void fx(int msk){
    int i,j;
    for(i=;i<k;i++)
    if(!(msk&(<<i))){
          fy(msk,i,);
          fy(msk,i,n-a[i]);
          for(j=;j<k;j++)
                 if(msk&(<<j)){
                        fy(msk,i,x[j]+a[i]);
                        fy(msk,i,x[j]-a[i]);
                 }
    }
}
class Posters {
    public:
      int maxCover(int wt,int ht,vector<int>pw,vector<int>ph){
         n=wt,m=ht,k=pw.size();
         for(int i=;i<k;i++){
           a[i]=min(pw[i],n);
           b[i]=min(ph[i],m);
         }
         fx();
         return ans;
      }
};