基于单决策树的AdaBoost

①起源：Boosting算法

Boosting算法的目的是每次基于全部数据集，通过使用同一种分类器不同的抽取参数方法（如决策树，每次都可以抽取不同的特征维度来剖分数据集）

训练一些不同弱分类器（单次分类错误率>0.5），然后将其组合起来，综合评估（默认认为每个分类器权重等价）进行分类。

AdaBoost算法进行了对其进行了改进。

一、每次训练分类器时，给予每条数据用于计算误差的不同权重D。

二、每个分类器，给予用于分类的不同权重alpha。

两种权的使用，使得AdaBoost在组合分类器时，能够根据当前的训练情况做一些调整。

②弱分类器：单决策树

单决策树应该是AdaBoost中使用最多的弱分类器。硬伤是单决策树是个0/1二类分类器。（实际是-1/+1二类）

一般决策树是通过DFS，连续选择不同维度多深度划分数据集。

单决策树就是一般决策树的1维版本，只搜dep=1就结束。

单决策树有两个好处：

一、单次分类效果很差（满足弱分类器定义）

二、根据决策属性不同，即便重复使用单决策树，也可以诞生出分类效果不同的分类器。

单决策树对于连续型数据，采用阈值（threshold）分类法。

首先确定所有数据中某个特征维度里的min/max范围。

然后采用步进的方法（每次阈值=min+当前步数*步长）来确定阈值。

基于同一个阈值，又可以把小于/大于阈值的分到不同类（2种分法）。

所以单决策树最多有【D*步数*2】种变形分类器。

②双权问题

一、分类器权alpha

定义 $\alpha = \frac{1}{2} \ln \left ( \frac{1-\varepsilon }{\varepsilon } \right )$，其中$\varepsilon$为错误率。

P.S 实际Coding时，为防止$\varepsilon$为零，通常取max($\varepsilon$，eps)

$\alpha$这个函数比较有趣，求导之后，假设每次使用新的分类器，错误率都会变小，以错误率变小为x正轴，有图像：

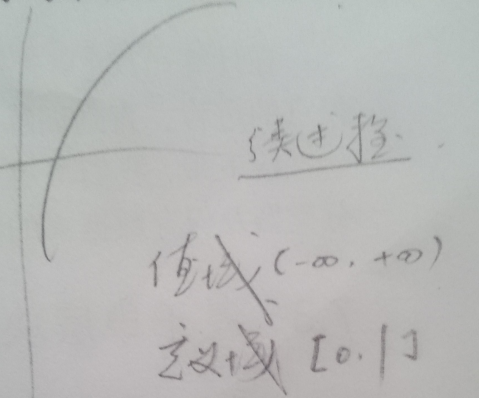
这个图像告诉我们，AdaBoost对后续分类器，给的权是逐渐变大的，因为我们有理由相信，后续分类器更科学一点。

分类器权如何使用呢？假设当前分类器的二类分类结果向量[-1,1,-1,1]，那么其加权之后就是$\alpha$ * [-1,1,-1,1]。

对于二类问题，将全部分类器的加权结果累加起来，通过判断加权结果符号的正负判断分类，因为$\alpha$的值域是R，所以只能看符号判断分类。

二、数据权D

每条数据都有权D，该权实际是个概率权，总权和=1。

如果一条数据被正确分类，则$D_{i}^{new}= \frac{D_{i}^{old}*e^{-\alpha}}{Sum(D)}$

如果一条数据被错误分类，则$D_{i}^{new}= \frac{D_{i}^{old}*e^{\alpha}}{Sum(D)}$

正确分类的权会被减小，错误分类的权会被增大。有趣的是，这两个式子如果单从$\alpha$角度来看，似乎有点问题。

如果某次$\alpha$为负，那么$D_{i}^{new}= \frac{D_{i}^{old}*e^{-\alpha}}{Sum(D)}$中$D_{i}^{new}$似乎好像是变大了。

但如果你把$\alpha$的定义式拉到$D_{i}^{new}$里面，就会发现：

$\left\{\begin{matrix}
D_{i}^{new}= \frac{1}{\sqrt{e}}*\frac{1-\varepsilon }{\varepsilon }
\\
D_{i}^{new}= \sqrt{e}*\frac{1-\varepsilon }{\varepsilon}
\end{matrix}\right.$

这样，很明显就可以看出，正确分类的权确实相对于错误分类的权被减小了。

数据权D的引入，主要是采用一种新的方式计算错误率。

一般的错误率$\varepsilon=\frac{errorExamples}{allExamples}$

但是AdaBoost里对错误率也进行加权了，$\varepsilon=\sum_{i=1}^{m}D_{i}*isError?1:0$

由于D是概率权，这样算出来的也算是错误率。如果一条数据分错了、又分错了、还是分错了，那么这条数据理应得到重视，其也会导致错误率比较大。

这种加权错误率对于在单决策树里，从众多变形分类器中，选择一个错误率最低分类器，有很好的参考意义。

③算法过程

★训练过程

while(true)

{

一、构建一个错误率最低的单决策树分类器，并保存记录该分类器全部属性（α、阀值、选取维度、分类结果）

二、利用构建的单决策树分类器计算α加权分类结果

若数据样本分类全部正确（大数据情况下几乎不可能）、分类正确率到达一定情况（多见于正确率收敛）则break

}

★测试过程

for（全部构建的分类器）

      for（全部测试数据）

           一、使用当前分类器分类

二、累计计算使用全部分类器的加权结果（记录α的原因）

根据加权结果的正负判断分类

不难发现，测试过程其实就是训练过程的某一步提取出来的。

④代码

#include "iostream"
#include "fstream"
#include "sstream"
#include "math.h"
#include "vector"
#include "string"
#include "cstdio"
using namespace std;
#define fin cin
#define inf 1e10
#define D dataSet[0].feature.size()
#define delta 100
int sign(double x) {return x<?-:;}
struct Data
{
    vector<double> feature;
    int y;
    Data(vector<double> feature,int y):feature(feature),y(y) {}
};
struct Stump
{
    vector<int> classEst;
    int dim,symbol;
    double threshold,error,alpha;
    Stump() {}
    Stump(vector<int> classEst,int dim,double threshold,int symbol,double error):classEst(classEst),dim(dim),threshold(threshold),symbol(symbol),error(error) {}
};
vector<Data> dataSet;
void read()
{
    ifstream fin("traindata.txt");
    string line;
    double fea,cls;
    int id;
    while(getline(cin,line))
    {
        vector<double> feature;
        stringstream sin(line);
        sin>>id;
        while(sin>>fea) feature.push_back(fea);
        cls=feature.back();feature.pop_back();
        dataSet.push_back(Data(feature,cls==?-:));
    }
}
vector<int> stumpClassify(int d,double threshold,int symbol)
{
    vector<int> ret(dataSet.size(),);
    for(int i=;i<dataSet.size();i++)
    {
        if(!symbol) {if(dataSet[i].feature[d]<=threshold) ret[i]=-;}
        else {if(dataSet[i].feature[d]>threshold) ret[i]=-;}
    }
    return ret;
}
Stump buildStump(vector<double> dataWeight)
{
    int step=;
    Stump bestStump;
    double minError=inf,weightError;
    for(int i=;i<D;i++)
    {
        double minRange=inf,maxRange=-inf,stepSize;
        for(int j=;j<dataSet.size();j++)
        {
            minRange=min(minRange,dataSet[j].feature[i]);
            maxRange=max(maxRange,dataSet[j].feature[i]);
        }
        stepSize=(maxRange-minRange)/step;
        for(int j=;j<=step;j++)
        {
            double threshold=minRange+stepSize*j;
            for(int k=;k<=;k++)
            {
                vector<int> classEst=stumpClassify(i,threshold,k);
                weightError=0.0;
                for(int t=;t<classEst.size();t++)
                    if(classEst[t]!=dataSet[t].y) weightError+=dataWeight[t];
                if(weightError<minError)
                {
                    bestStump=Stump(classEst,i,threshold,k,weightError);
                    minError=weightError;
                }
            }
        }
    }
    return bestStump;
}
vector<Stump> mainProcess()
{
    int iter=,repeat=,last_cnt=-;
    vector<double> dataWeight(dataSet.size(),1.0/dataSet.size());
    vector<double> aggClassEst(dataSet.size(),0.0);
    vector<Stump> stumpList;
    while()
    {
        iter++;
        Stump nowStump=buildStump(dataWeight);
        double alpha=0.5*log((1.0-nowStump.error)/max(nowStump.error,1e-)),DSum=0.0;
        nowStump.alpha=alpha;
        stumpList.push_back(nowStump);
        int err_cnt=;
        for(int i=;i<dataSet.size();i++)
        {
            double ret=-*alpha*dataSet[i].y*nowStump.classEst[i];
            dataWeight[i]=dataWeight[i]*exp(ret);
            DSum+=dataWeight[i];
        }
        for(int i=;i<dataSet.size();i++)
        {
            dataWeight[i]/=DSum;
            aggClassEst[i]+=alpha*nowStump.classEst[i];
            if(sign(aggClassEst[i])!=dataSet[i].y) err_cnt++;
        }
        //cout<<err_cnt<<"/"<<dataSet.size()<<endl;
        if(err_cnt!=last_cnt) {last_cnt=err_cnt;repeat=;}
        else repeat++;
        if(err_cnt==||repeat>delta) break;
    }
    return stumpList;
}
void classify(vector<Stump> stumpList)
{
    ifstream fin("testdata.txt");
    dataSet.clear();
    string line;
    double fea,cls;
    int id;
    while(getline(cin,line))
    {
        vector<double> feature;
        stringstream sin(line);
        sin>>id;
        while(sin>>fea) feature.push_back(fea);
        cls=feature.back();feature.pop_back();
        dataSet.push_back(Data(feature,cls==?-:));
    }
    vector<double> aggClassEst(dataSet.size(),0.0);
    for(int i=;i<stumpList.size();i++)
    {
        vector<int> classEst=stumpClassify(stumpList[i].dim,stumpList[i].threshold,stumpList[i].symbol);
        for(int j=;j<dataSet.size();j++)
          aggClassEst[j]+=(stumpList[i].alpha*classEst[j]);
    }
    for(int i=;i<dataSet.size();i++)
        if(sign(aggClassEst[i])==-) printf("%test #%d:  origin: %d class %d\n",i,dataSet[i].y,-);
        else printf("%test #%d: origin: %d class %d\n",i,dataSet[i].y,);
}
int main()
{
    read();
    vector<Stump> stumpList=mainProcess();
    classify(stumpList);
}