【OpenCV】边缘检测：Sobel、拉普拉斯算子

推荐博文，博客。写得很好，给个赞。

Reference Link ： http://blog.csdn.net/xiaowei_cqu/article/details/7829481

一阶导数法：梯度算子

 

对于左图，左侧的边是正的（由暗到亮），右侧的边是负的（由亮到暗）。对于右图，结论相反。常数部分为零。用来检测边是否存在。

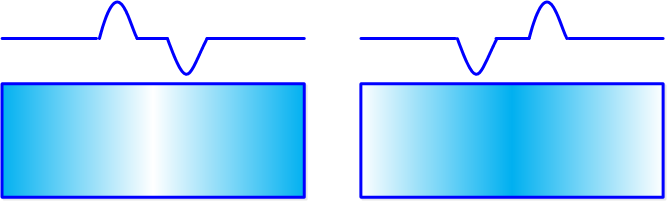
梯度算子 Gradient operators

函数f(x,y)在(x,y)处的梯度为一个向量：

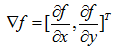
计算这个向量的大小为：

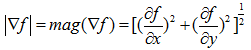
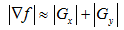
梯度的方向角为：

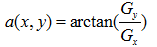
Sobel算子

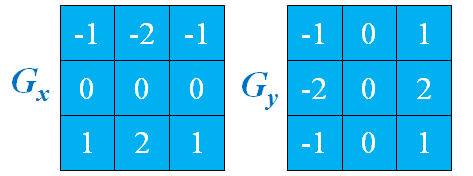
sobel算子的表示：

梯度幅值：

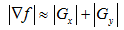
用卷积模板来实现：

【相关代码】

1. CV_EXPORTS_W  Sobel( InputArray src, OutputArray dst,  ddepth,
2. ksize=3,
3. double scale=1, double delta=0,
4. borderType=BORDER_DEFAULT );

CV_EXPORTS_W void Sobel( InputArray src, OutputArray dst, int ddepth,
                         int dx, int dy, int ksize=3,
                         double scale=1, double delta=0,
                         int borderType=BORDER_DEFAULT );

1. /////////////////////////// Sobe l////////////////////////////////////
2. /// Generate grad_x and grad_y
3. Mat grad_x, grad_y;
4. Mat abs_grad_x, abs_grad_y;
5. /// Gradient X
6. //Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );
7. //Calculates the first, second, third, or mixed image derivatives using an extended Sobel operator.
8. Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
9. convertScaleAbs( grad_x, abs_grad_x );
10. /// Gradient Y
11. //Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );
12. Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
13. convertScaleAbs( grad_y, abs_grad_y );
14. /// Total Gradient (approximate)
15. addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );

  /////////////////////////// Sobe l////////////////////////////////////
  /// Generate grad_x and grad_y
  Mat grad_x, grad_y;
  Mat abs_grad_x, abs_grad_y;
  /// Gradient X
  //Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );
  //Calculates the first, second, third, or mixed image derivatives using an extended Sobel operator.
  Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
  convertScaleAbs( grad_x, abs_grad_x );
  /// Gradient Y
  //Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );
  Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
  convertScaleAbs( grad_y, abs_grad_y );
  /// Total Gradient (approximate)
  addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );

二阶微分法：拉普拉斯

二阶微分在亮的一边是负的，在暗的一边是正的。常数部分为零。可以用来确定边的准确位置，以及像素在亮的一侧还是暗的一侧。

LapLace 拉普拉斯算子

二维函数f(x,y)的拉普拉斯是一个二阶的微分，定义为：

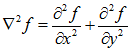
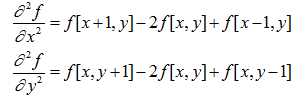
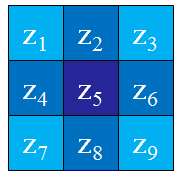
可以用多种方式将其表示为数字形式。对于一个3*3的区域，经验上被推荐最多的形式是：

定义数字形式的拉普拉斯要求系数之和必为0

【相关代码】

1. CV_EXPORTS_W  Laplacian( InputArray src, OutputArray dst,  ddepth,
2. ksize=1, double scale=1, double delta=0,
3. borderType=BORDER_DEFAULT );

CV_EXPORTS_W void Laplacian( InputArray src, OutputArray dst, int ddepth,
                             int ksize=1, double scale=1, double delta=0,
                             int borderType=BORDER_DEFAULT );

1. Mat abs_dst,dst;
2. scale = 1;
3. delta = 0;
4. ddepth = CV_16S;
5. kernel_size = 3;
6. Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );
7. convertScaleAbs( dst, abs_dst );
8. namedWindow( window_name2, CV_WINDOW_AUTOSIZE );

Mat abs_dst,dst;
  int scale = 1;
  int delta = 0;
  int ddepth = CV_16S;
  int kernel_size = 3;
  Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );
  convertScaleAbs( dst, abs_dst );
  namedWindow( window_name2, CV_WINDOW_AUTOSIZE );

注意，边缘检测对噪声比较敏感，需要先用高斯滤波器对图像进行平滑。参考博文：【OpenCV】邻域滤波：方框、高斯、中值、双边滤波

Sobel 边缘检测

Sobel算子可以直接计算Gx 、Gy可以检测到边的存在，以及从暗到亮，从亮到暗的变化。仅计算| Gx |，产生最强的响应是正交 于x轴的边； | Gy |则是正交于y轴的边。

Laplace边缘检测

拉普拉斯对噪声敏感，会产生双边效果。不能检测出边的方向。通常不直接用于边的检测，只起辅助的角色，检测一个像素是在边的亮的一边还是暗的一边利用零跨越，确定边的位置。

转载请注明出处：http://blog.csdn.net/xiaowei_cqu/article/details/7829481

实验代码下载：http://download.csdn.net/detail/xiaowei_cqu/4475976