神经网络入门篇：激活函数（Activation functions）

激活函数

使用一个神经网络时，需要决定使用哪种激活函数用隐藏层上，哪种用在输出节点上。到目前为止，之前的博客只用过sigmoid激活函数，但是，有时其他的激活函数效果会更好。

在神经网路的前向传播中，\(a^{[1]} = \sigma(z^{[1]})\)和\(a^{[2]} =\sigma(z^{[2]})\)这两步会使用到sigmoid函数。sigmoid函数在这里被称为激活函数。

公式1.18：

\(a = \sigma(z) = \frac{1}{{1 + e}^{- z}}\)

更通常的情况下，使用不同的函数\(g( z^{[1]})\)，\(g\)可以是除了sigmoid函数以外的非线性函数。tanh函数或者双曲正切函数是总体上都优于sigmoid函数的激活函数。

如图，\(a = tan(z)\)的值域是位于+1和-1之间。

公式1.19：

\(a= tanh(z) = \frac{e^{z} - e^{- z}}{e^{z} + e^{- z}}\)

事实上，tanh函数是sigmoid的向下平移和伸缩后的结果。对它进行了变形后，穿过了\((0,0)\)点，并且值域介于+1和-1之间。

结果表明，如果在隐藏层上使用函数

公式1.20：

$g(z^{[1]}) = tanh(z^{[1]}) $

效果总是优于sigmoid函数。因为函数值域在-1和+1的激活函数，其均值是更接近零均值的。在训练一个算法模型时，如果使用tanh函数代替sigmoid函数中心化数据，使得数据的平均值更接近0而不是0.5.

这会使学习下一层简单一点。

在讨论优化算法时，有一点要说明：我基本已经不用sigmoid激活函数了，tanh函数在所有场合都优于sigmoid函数。

但有一个例外：在二分类的问题中，对于输出层，因为\(y\)的值是0或1，所以想让\(\hat{y}\)的数值介于0和1之间，而不是在-1和+1之间。所以需要使用sigmoid激活函数。这里的

公式1.21：

\(g(z^{[2]}) = \sigma(z^{[2]})\)

在这个例子里看到的是，对隐藏层使用tanh激活函数，输出层使用sigmoid函数。

所以，在不同的神经网络层中，激活函数可以不同。为了表示不同的激活函数，在不同的层中，使用方括号上标来指出\(g\)上标为\([1]\)的激活函数，可能会跟\(g\)上标为\([2]\)不同。方括号上标\([1]\)代表隐藏层，方括号上标\([2]\)表示输出层。

sigmoid函数和tanh函数两者共同的缺点是，在\(z\)特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于0，导致降低梯度下降的速度。

在机器学习另一个很流行的函数是：修正线性单元的函数（ReLu），ReLu函数图像是如下图。

公式1.22：

\(a =max(0,z)\)

所以，只要\(z\)是正值的情况下，导数恒等于1，当\(z\)是负值的时候，导数恒等于0。从实际上来说，当使用\(z\)的导数时，\(z\)=0的导数是没有定义的。但是当编程实现的时候，\(z\)的取值刚好等于0.00000001，这个值相当小，所以，在实践中，不需要担心这个值，\(z\)是等于0的时候，假设一个导数是1或者0效果都可以。

这有一些选择激活函数的经验法则：

如果输出是0、1值（二分类问题），则输出层选择sigmoid函数，然后其它的所有单元都选择Relu函数。

这是很多激活函数的默认选择，如果在隐藏层上不确定使用哪个激活函数，那么通常会使用Relu激活函数。有时，也会使用tanh激活函数，但Relu的一个优点是：当\(z\)是负值的时候，导数等于0。

这里也有另一个版本的Relu被称为Leaky Relu。

当\(z\)是负值时，这个函数的值不是等于0，而是轻微的倾斜，如图。

这个函数通常比Relu激活函数效果要好，尽管在实际中Leaky ReLu使用的并不多。

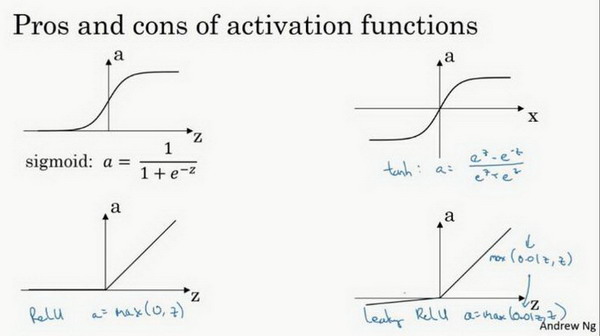
图1.6.1

两者的优点是：

第一，在\(z\)的区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于0，在程序实现就是一个if-else语句，而sigmoid函数需要进行浮点四则运算，在实践中，使用ReLu激活函数神经网络通常会比使用sigmoid或者tanh激活函数学习的更快。

第二，sigmoid和tanh函数的导数在正负饱和区的梯度都会接近于0，这会造成梯度弥散，而Relu和Leaky ReLu函数大于0部分都为常数，不会产生梯度弥散现象。(同时应该注意到的是，Relu进入负半区的时候，梯度为0，神经元此时不会训练，产生所谓的稀疏性，而Leaky ReLu不会有这问题)

\(z\)在ReLu的梯度一半都是0，但是，有足够的隐藏层使得z值大于0，所以对大多数的训练数据来说学习过程仍然可以很快。

快速概括一下不同激活函数的过程和结论。

• sigmoid激活函数：除了输出层是一个二分类问题基本不会用它。

• tanh激活函数：tanh是非常优秀的，几乎适合所有场合。

• ReLu激活函数：最常用的默认函数，如果不确定用哪个激活函数，就使用ReLu或者Leaky ReLu。

公式3.23：

\(a = max( 0.01z,z)\)

为什么常数是0.01？当然，可以为学习算法选择不同的参数。

在选择自己神经网络的激活函数时，有一定的直观感受，在深度学习中的经常遇到一个问题：在编写神经网络的时候，会有很多选择：隐藏层单元的个数、激活函数的选择、初始化权值……这些选择想得到一个对比较好的指导原则是挺困难的。

鉴于以上三个原因，以及在工业界的见闻，提供一种直观的感受，哪一种工业界用的多，哪一种用的少。但是，自己的神经网络的应用，以及其特殊性，是很难提前知道选择哪些效果更好。所以通常的建议是：如果不确定哪一个激活函数效果更好，可以把它们都试试，然后在验证集或者发展集上进行评价。然后看哪一种表现的更好，就去使用它。

为自己的神经网络的应用测试这些不同的选择，会在以后检验自己的神经网络或者评估算法的时候，看到不同的效果。如果仅仅遵守使用默认的ReLu激活函数，而不要用其他的激励函数，那就可能在近期或者往后，每次解决问题的时候都使用相同的办法。