#计数，记忆化搜索#C 连边方案

---

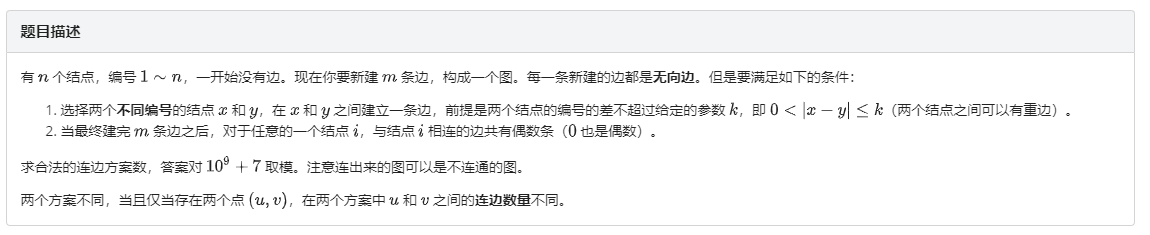
分析

设\(dp[i][j][k][l]\)表示处理到\([i-l+1,i]\)的连边，二进制状态（奇点还是偶点）为\(k\)的方案数，

最后一维是为了避免算重，那么如果第\(i-l+1\)位是偶点可以转移到\(i+1\)，否则枚举连边即可

---

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#define rr register
using namespace std;
const int mod=1000000007; int nn,mm,k,dp[32][32][511][10];
inline signed mo(int x,int y){return x+y>=mod?x+y-mod:x+y;}
inline signed dfs(int n,int m,int S,int now){
	if (~dp[n][m][S][now]) return dp[n][m][S][now];
	if (n==nn+1) return m==mm;
	rr int ans=0;
	if (!(S&1)) ans=mo(ans,dfs(n+1,m,S>>1,1));
	if (m<mm){
		rr int lim=min(k,nn-n);
		for (rr int i=now;i<=lim;++i)
		    ans=mo(ans,dfs(n,m+1,S^1^(1<<i),i));
	}
	return dp[n][m][S][now]=ans;
}
signed main(){
	freopen("graph.in","r",stdin);
	freopen("graph.out","w",stdout);
	scanf("%d%d%d",&nn,&mm,&k);
	memset(dp,-1,sizeof(dp));
	return !printf("%d",dfs(1,0,0,1));
}