线段树（SegmentTree）

• 对于数组应用于区间染色实现为On，而线段树是O(logn)

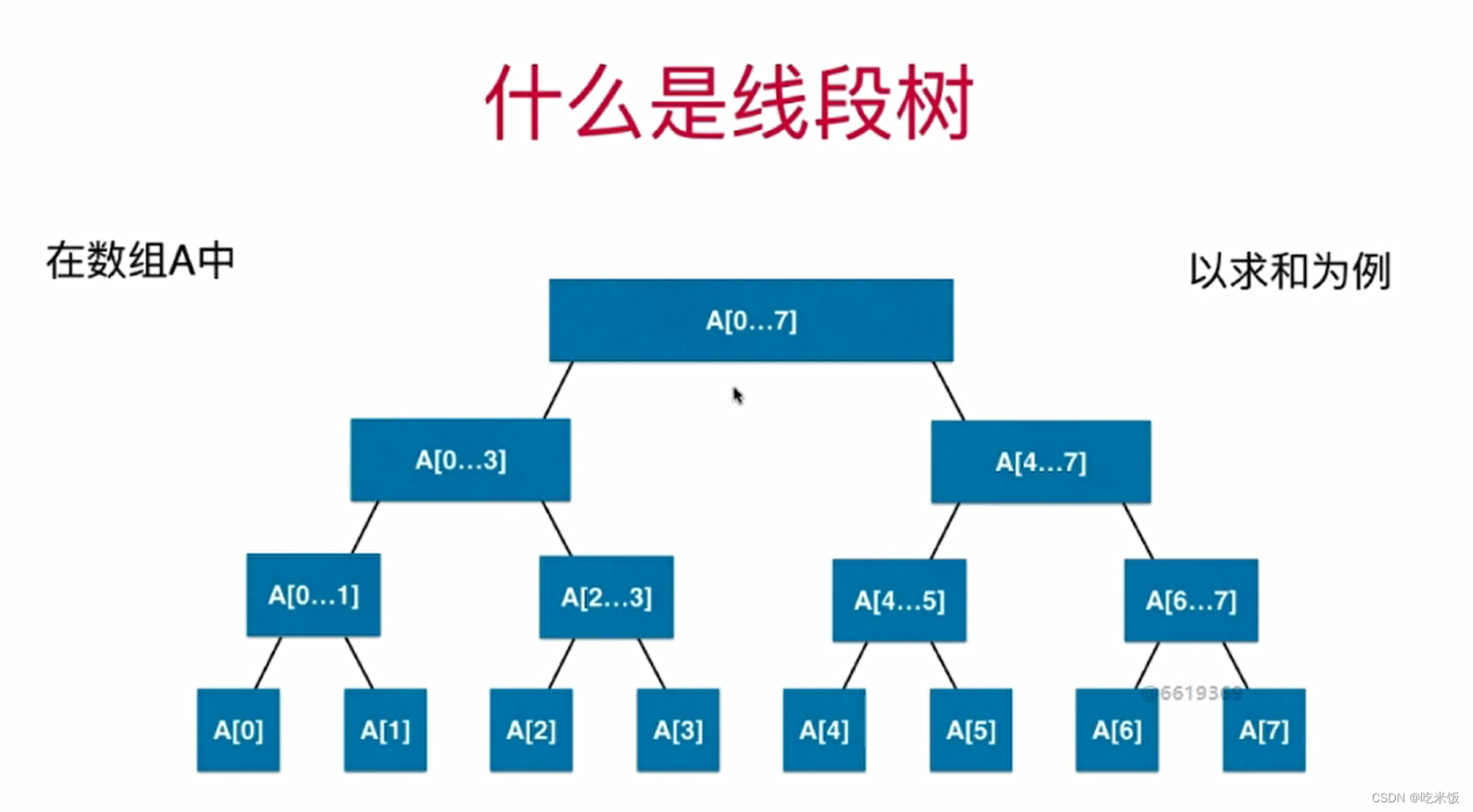
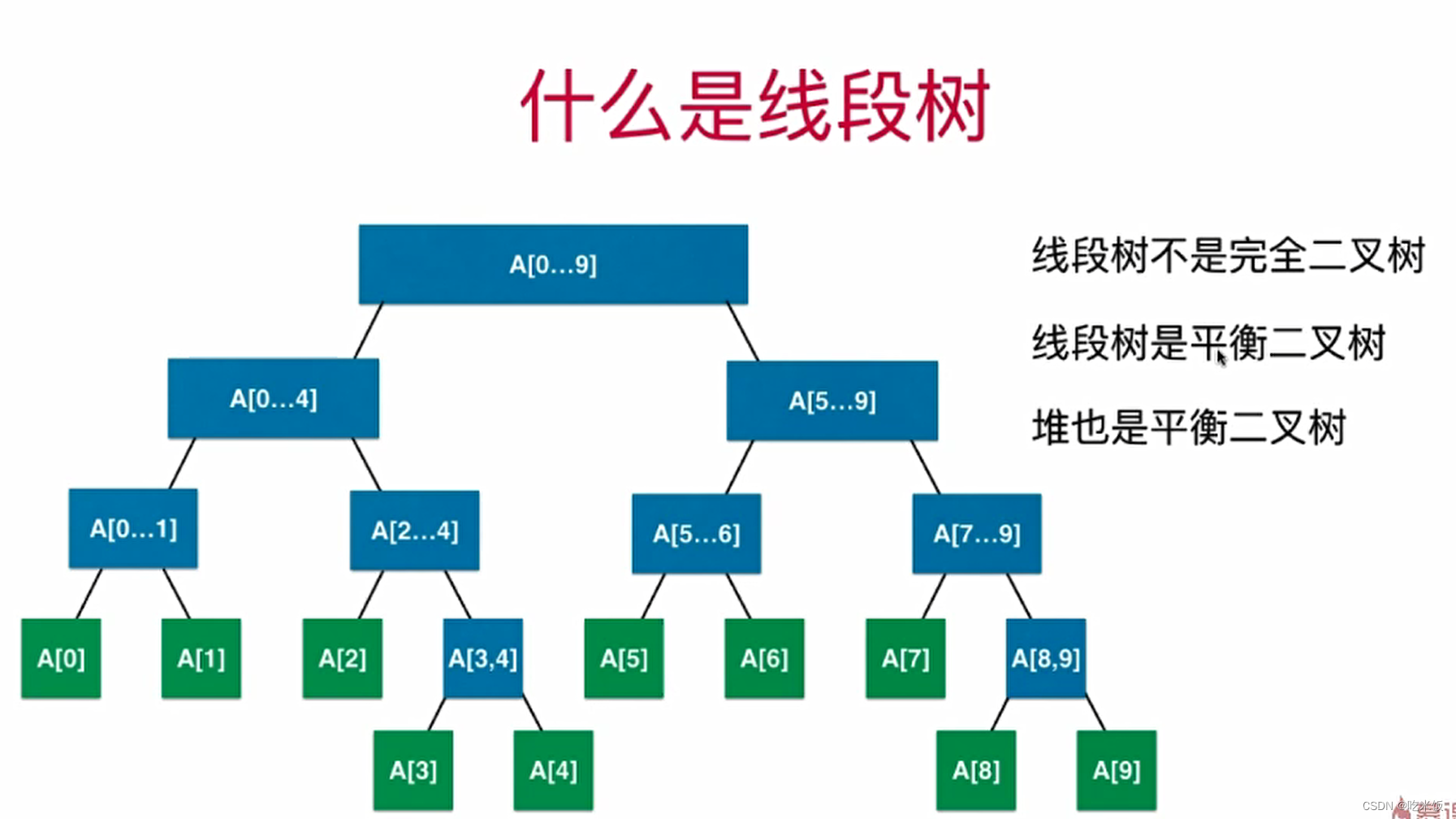
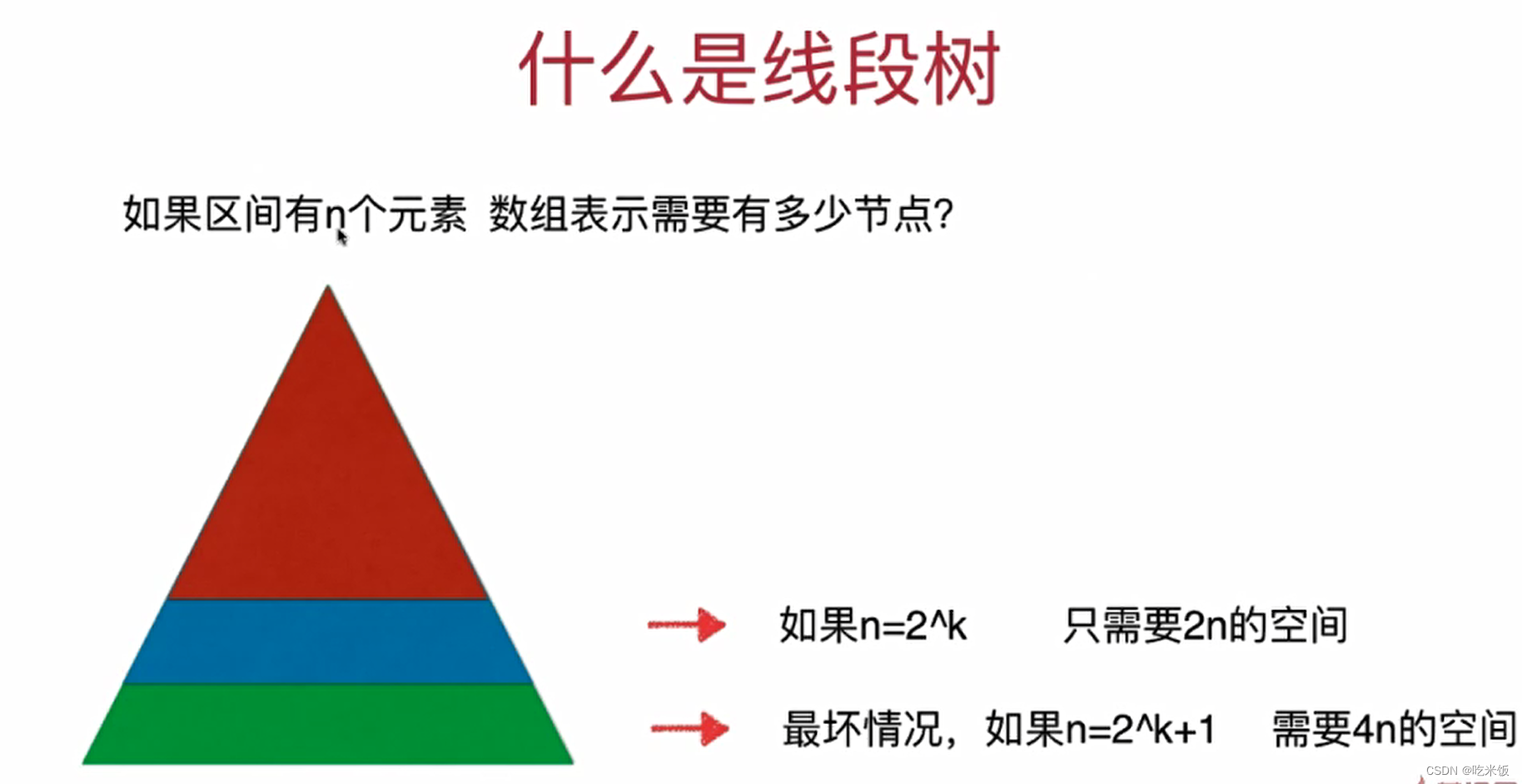
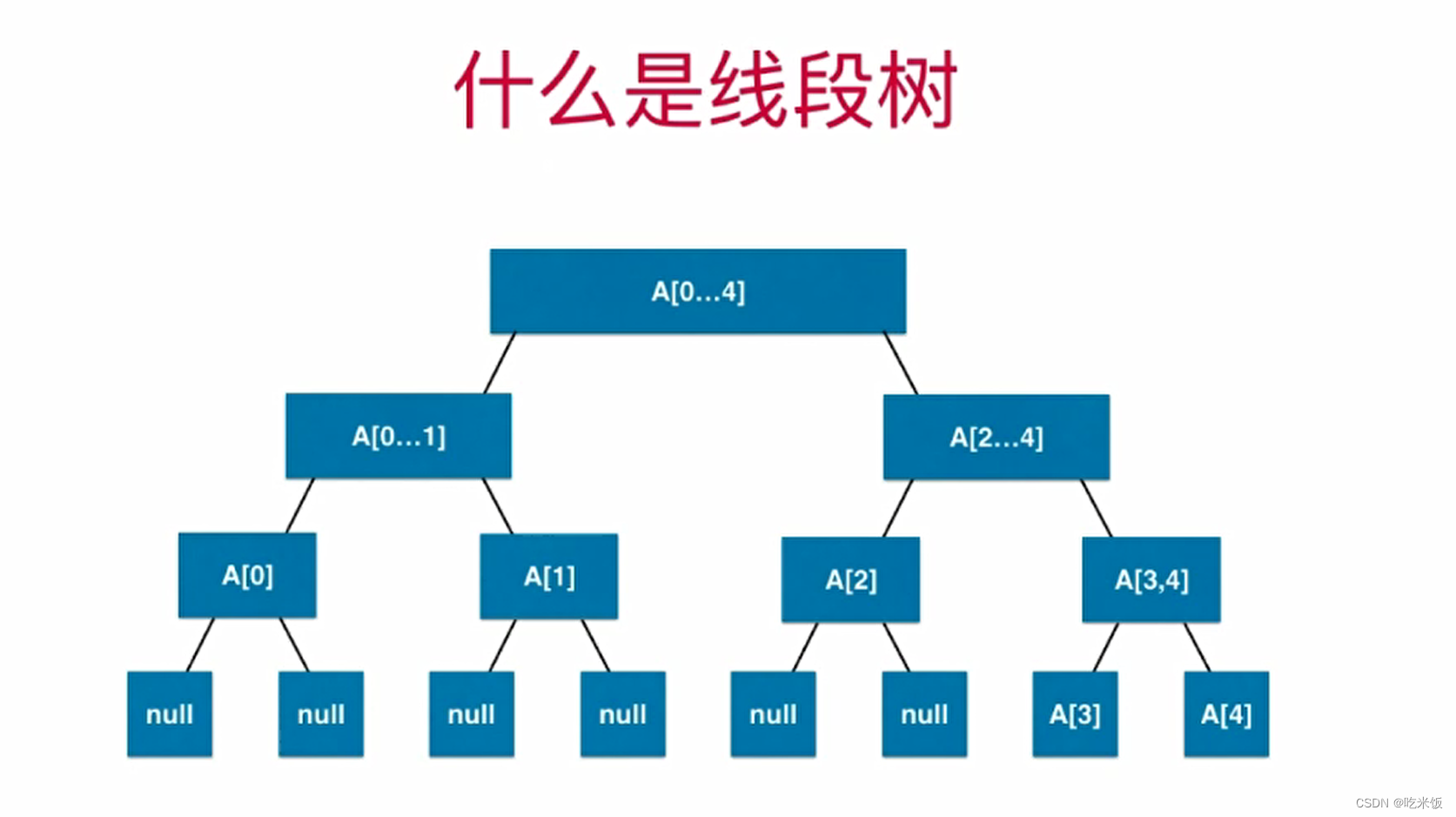
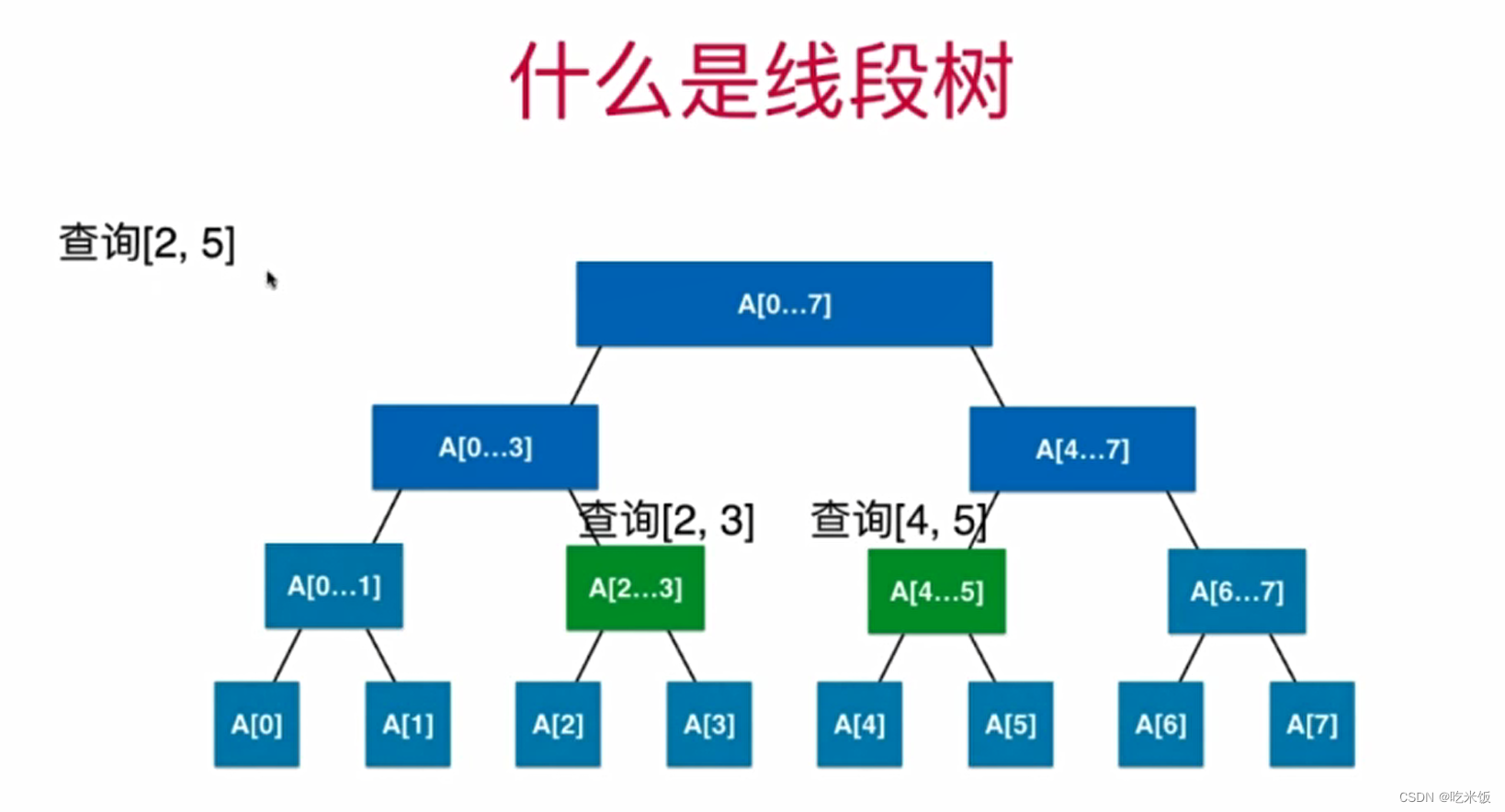
• 什么是线段树：对于一个二叉树，每一个节点存储的是一个线段或是一个区间相应的信息。
  
  
  
  
  
  
  
  
  
  

查询

更新

#pragma once

#include <cassert>
#include <functional>

template<typename T>
class SegmentTree {
public:
    SegmentTree() noexcept = default;

    explicit SegmentTree(const T *const arr, const int n, std::function<T(T, T)> func) : data(new T[n]),
                                                                                         tree(new T[4 * n]),
                                                                                         size(n),
                                                                                         function(func) {
        for (int i = 0; i < n; ++i) {
            data[i] = arr[i];
        }
        //构建线段树 根索引为0，左边界为0，有边界为 size-1
        buildSegmentTree(0, 0, size - 1);
    }

    ~SegmentTree() noexcept {
        delete[] data;
        data = nullptr;
        delete[] tree;
        tree = nullptr;
    }

    constexpr int getSize() const noexcept {
        return size;
    }

    T get(const int index) const {
        assert(index >= 0 && index < size);
        return data[index];
    }

    T query(const int queryL, const int queryR) {
        assert(queryL >= 0 && queryL < size && queryR >= 0 && queryR < size && queryL <= queryR);
        return query(0, 0, size - 1, queryL, queryR);
    }

    void set(const int index, const T &e) {
        assert(index >= 0 && index < size);
        data[index] = e;
        set(0, 0, size - 1, index, e);
    }

    void print() const {
        std::cout << "[";
        for (int i = 0; i < size * 4; ++i) {
            if (tree[i] != NULL) {
                std::cout << tree[i];
            } else {
                std::cout << "0";
            }
            if (i != size * 4 - 1) {
                std::cout << ", ";
            }
        }
        std::cout << "]" << std::endl;
    }

private:

    void set(const int treeIndex, const int l, const int r, const int index, const T &e) {
        //都叶子了，一定是它了，更新它
        if (l == r) {
            tree[treeIndex] = e;
            return;
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        //要找的索引大于中间值，一定在右边
        if (index >= mid + 1) {
            set(rightTreeIndex, mid + 1, r, index, e);
        } else if (index <= mid) {  //否则在左边
            set(leftTreeIndex, l, mid, index, e);
        }
        //更新...
        tree[treeIndex] = function(tree[leftTreeIndex], tree[rightTreeIndex]);
    }

    //在以treeIndex为根的线段树[l...r]的范围里，搜索区间[queryL,queryR]的值
    int query(const int treeIndex, const int l, const int r, const int queryL, const int queryR) {
        //如果左右相同就找到了
        if (l == queryL && r == queryR) {
            return tree[treeIndex];
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        //如果查找的范围左边界大于中间
        if (mid + 1 <= queryL) {
            //那么就不用查找左边
            return query(rightTreeIndex, mid + 1, r, queryL, queryR);
            //如果查找的范围右边小于中间
        } else if (mid >= queryR) {
            //那么就不用查找右边
            return query(leftTreeIndex, l, mid, queryL, queryR);
        }
        //如果查找的范围占用两个区间
        T leftResult = query(leftTreeIndex, l, mid, queryL, mid);
        T rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
        return function(leftResult, rightResult);
    }

    void buildSegmentTree(const int treeIndex, const int left, const int right) {
        //如果左右相等就说明递归到底
        if (left == right) {
            tree[treeIndex] = data[left];
            return;
        }
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        int mid = left + (right - left) / 2;
        //递归左右孩子根为左右孩子索引，左右边界以中间为界
        buildSegmentTree(leftTreeIndex, left, mid);
        buildSegmentTree(rightTreeIndex, mid + 1, right);
        //线段存储信息根据业务写相应的代码，以求和为例，
        tree[treeIndex] = function(tree[leftTreeIndex], tree[rightTreeIndex]);
    }

    constexpr int leftChild(const int index) const noexcept {
        return index * 2 + 1;
    }

    constexpr int rightChild(const int index) const noexcept {
        return index * 2 + 2;
    }

private:
    std::function<T(T, T)> function;
    T *tree;
    T *data;
    int size;
};

#include <iostream>
#include "SegmentTree.h"

int main() {
    int nums[] = {-2, 0, 3, -5, 2, -1};
    SegmentTree<int> *segmentTree = new SegmentTree<int>(nums, sizeof(nums) / sizeof(int), [](int a, int b) -> int {
        return a + b;
    });
    std::cout << segmentTree->query(0,2) << std::endl;
    std::cout << segmentTree->query(2,5) << std::endl;
    std::cout << segmentTree->query(0,5) << std::endl;
    segmentTree->print();
    segmentTree->set(0,0);
    segmentTree->print();
    std::cout << segmentTree->query(0,2) << std::endl;
    std::cout << segmentTree->query(2,5) << std::endl;
    std::cout << segmentTree->query(0,5) << std::endl;

    return 0;
}

输出
1
-1
-3
[-3, 1, -4, -2, 3, -3, -1, -2, 0, 0, 0, -5, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[-1, 3, -4, 0, 3, -3, -1, 0, 0, 0, 0, -5, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3
-1
-1

LeetCode

307. 区域和检索 - 数组可修改

给你一个数组 nums ，请你完成两类查询。

1. 其中一类查询要求 更新 数组 nums 下标对应的值
2. 另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 ，其中 left <= right
   
   实现 NumArray 类：

• NumArray(int[] nums) 用整数数组 nums 初始化对象
• void update(int index, int val) 将 nums[index] 的值 更新 为 val
• int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 （即，nums[left] + nums[left + 1], ..., nums[right]）

class NumArray
{
public:
    NumArray(vector<int> nums)
    {
        if (nums.size() > 0)
        {
            int *data = new int[nums.size()];
            for (int i = 0; i < nums.size(); ++i)
            {
                data[i] = nums[i];
            }
            segmentTree = new SegmentTree<int>(data, nums.size(), [](int a, int b) -> int
                                               { return a + b; });
        }
    }

    void update(int i, int val)
    {
        assert(segmentTree != nullptr);
        segmentTree->set(i, val);
    }

    int sumRange(int i, int j)
    {
        assert(segmentTree != nullptr);
        return segmentTree->query(i, j);
    }

private:
    template<typename T>
    class SegmentTree {
    public:
        SegmentTree() noexcept = default;

        explicit SegmentTree(const T *const arr, const int n, std::function<T(T, T)> func) : data(new T[n]),
                                                                                            tree(new T[4 * n]),
                                                                                            size(n),
                                                                                            function(func) {
            for (int i = 0; i < n; ++i) {
                data[i] = arr[i];
            }
            //构建线段树 根索引为0，左边界为0，有边界为 size-1
            buildSegmentTree(0, 0, size - 1);
        }

        ~SegmentTree() noexcept {
            delete[] data;
            data = nullptr;
            delete[] tree;
            tree = nullptr;
        }

        constexpr int getSize() const noexcept {
            return size;
        }

        T get(const int index) const {
            assert(index >= 0 && index < size);
            return data[index];
        }

        T query(const int queryL, const int queryR) {
            assert(queryL >= 0 && queryL < size && queryR >= 0 && queryR < size && queryL <= queryR);
            return query(0, 0, size - 1, queryL, queryR);
        }

        void set(const int index, const T &e) {
            assert(index >= 0 && index < size);
            data[index] = e;
            set(0, 0, size - 1, index, e);
        }

        void print() const {
            std::cout << "[";
            for (int i = 0; i < size * 4; ++i) {
                if (tree[i] != NULL) {
                    std::cout << tree[i];
                } else {
                    std::cout << "0";
                }
                if (i != size * 4 - 1) {
                    std::cout << ", ";
                }
            }
            std::cout << "]" << std::endl;
        }

    private:

        void set(const int treeIndex, const int l, const int r, const int index, const T &e) {
            //都叶子了，一定是它了，更新它
            if (l == r) {
                tree[treeIndex] = e;
                return;
            }
            int mid = l + (r - l) / 2;
            int leftTreeIndex = leftChild(treeIndex);
            int rightTreeIndex = rightChild(treeIndex);
            //要找的索引大于中间值，一定在右边
            if (index >= mid + 1) {
                set(rightTreeIndex, mid + 1, r, index, e);
            } else if (index <= mid) {  //否则在左边
                set(leftTreeIndex, l, mid, index, e);
            }
            //更新...
            tree[treeIndex] = function(tree[leftTreeIndex], tree[rightTreeIndex]);
        }

        //在以treeIndex为根的线段树[l...r]的范围里，搜索区间[queryL,queryR]的值
        int query(const int treeIndex, const int l, const int r, const int queryL, const int queryR) {
            //如果左右相同就找到了
            if (l == queryL && r == queryR) {
                return tree[treeIndex];
            }
            int mid = l + (r - l) / 2;
            int leftTreeIndex = leftChild(treeIndex);
            int rightTreeIndex = rightChild(treeIndex);
            //如果查找的范围左边界大于中间
            if (mid + 1 <= queryL) {
                //那么就不用查找左边
                return query(rightTreeIndex, mid + 1, r, queryL, queryR);
                //如果查找的范围右边小于中间
            } else if (mid >= queryR) {
                //那么就不用查找右边
                return query(leftTreeIndex, l, mid, queryL, queryR);
            }
            //如果查找的范围占用两个区间
            T leftResult = query(leftTreeIndex, l, mid, queryL, mid);
            T rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
            return function(leftResult, rightResult);
        }

        void buildSegmentTree(const int treeIndex, const int left, const int right) {
            //如果左右相等就说明递归到底
            if (left == right) {
                tree[treeIndex] = data[left];
                return;
            }
            int leftTreeIndex = leftChild(treeIndex);
            int rightTreeIndex = rightChild(treeIndex);
            int mid = left + (right - left) / 2;
            //递归左右孩子根为左右孩子索引，左右边界以中间为界
            buildSegmentTree(leftTreeIndex, left, mid);
            buildSegmentTree(rightTreeIndex, mid + 1, right);
            //线段存储信息根据业务写相应的代码，以求和为例，
            tree[treeIndex] = function(tree[leftTreeIndex], tree[rightTreeIndex]);
        }

        constexpr int leftChild(const int index) const noexcept {
            return index * 2 + 1;
        }

        constexpr int rightChild(const int index) const noexcept {
            return index * 2 + 2;
        }

    private:
        std::function<T(T, T)> function;
        T *tree;
        T *data;
        int size;
    };
    SegmentTree<int> *segmentTree;
};