leetcode(力扣) 2866. 美丽塔 II

原题链接

暴力做法 (时间复杂度 O(n^2))

每次选取下标 i 为峰值, 进行 n 次，对每次取max就可以找到答案

---

对于 i 左边的序列: 需要满足序列是非递减的, 同时每个值尽可能大

所以满足: j 的位置上的数 <= (j, i] 上的最小的值 (等于时取得最大值) , 同时需要保证 j 位置上的数要小于heights[j] (题目中的要求，美丽塔的要求); 即 t = min(pre, heights[j]) pre表示的是 下标是 (j, i] 的最小的值

---

对于 i 右边的序列: 需要满足序列是非递增的，同时每个值尽可能大

所以满足：j 的位置上的数 <= [i, j) 上的最小的值 (等于时取得最大值), 同时需要保证 j 位置上的数要小于heights[j]； 即 t = min(pre, heights[j]) pre表示的是 下标是 [i, j) 的最小的值

class Solution {
public:
    long long maximumSumOfHeights(vector<int>& heights) {
        int n = heights.size();
        long long res = 0;
        for (int i = 0; i < n; i ++ )
        {
            int pre = heights[i];
            long long sum = heights[i] * 1LL;
            for (int j = i - 1; j >= 0; j --)  // pre表示的是下标 (j, i] 中heights中的最小值
            {
                sum += min(pre, heights[j]);    // 下标从i - 1开始， 每次取min，可以保证当下标为 j 时 pre 表示的就是 [j + 1, i] 的最小值
                pre = min(pre, heights[j]);
            }
            pre = heights[i];
            for (int j = i + 1; j < n; j ++)  // pre表示的是下标 [i, j) 中heights中的最小值
            {
                sum += min(pre, heights[j]);
                pre = min(pre, heights[j]);
            }
            res = max(sum, res);
        }
        return res;
    }
};

---

单调栈做法 (时间复杂度 O(n)) (tag: 单调栈、 动态规划)

st1 和 st2 存的都是下标

下面图片模拟的是 第一个 for循环， 标红的是 进入 if(st1.empty()) 这个分支的

p1[4] 为什么加的是 2 x heights[4]呢， 因为此时st1中还有 元素1的下标2， 此时 下标3 和 下标4 的高度应该都为heights[4]

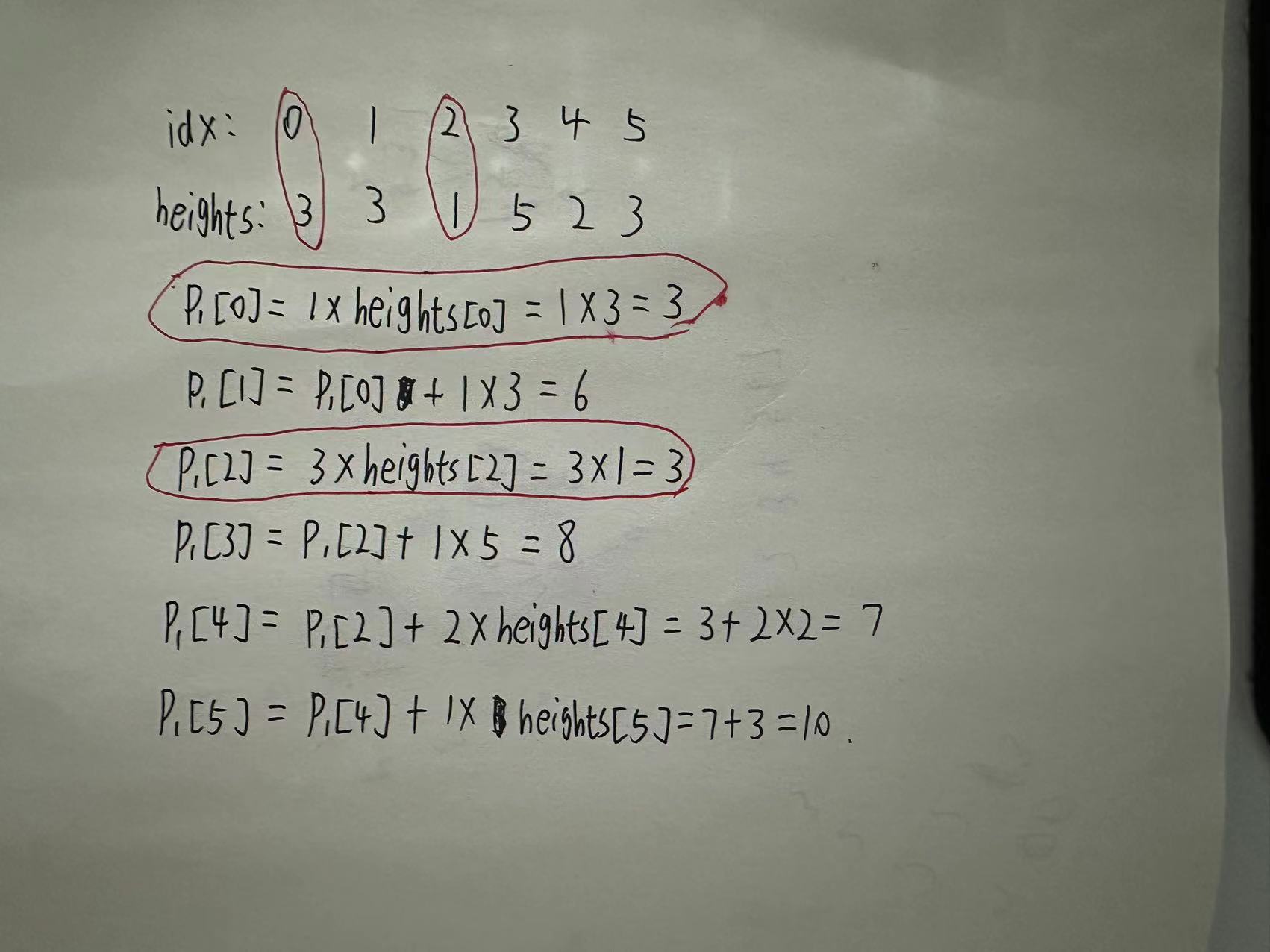
class Solution {
public:
    long long maximumSumOfHeights(vector<int>& heights) {
        int n = heights.size();

        long long res = 0;
        stack<int> st1; stack<int> st2;  // 栈里面存的是 下标
        vector<long long> p1(n); vector<long long> p2(n);
        // p1 的状态表示是 下标为 i 的 左侧美丽塔高度之和 (包含i本身，同时满足p1[i]是美丽塔高度和的最大值)
        // p2 的状态表示是 下标为 i 的 右侧美丽塔高度之和 (包含i本身，同时满足p1[i]是美丽塔高度和的最大值)

        for (int i = 0; i < n; i ++)
        {
            while (!st1.empty() && heights[i] < heights[st1.top()]) st1.pop(); // 让栈满足 (栈为空 || 栈中元素对应的heights的值是非递减的)

           // 栈为空 说明 : i = 0或者 i 前面的山脉高度都比 heights[i] 大， 为了保证序列非递减, 前面的所有数都应该是 heights[i]
            if (st1.empty()) p1[i] = (long long)(i + 1) * heights[i];
            else p1[i] = p1[st1.top()]  + (long long)(i - st1.top()) * heights[i] ;
          // 不为空 说明 下标为 (st1.top(), i] 山脉高度 都比 heights[i] 大， 为了保证序列非递减,  (st1.top(), i] 之间的山脉高度都应该是  heights[i]

            st1.emplace(i);
        }

        for (int i = n - 1; i >= 0; i --)  // 需要保证从后往前是一个非递减序列
        {
            while (!st2.empty() && heights[i] < heights[st2.top()]) st2.pop(); 

            if (st2.empty()) p2[i] = (long long)(n - i) * heights[i] * 1LL;
            else p2[i] = p2[st2.top()] + (long long)(st2.top() - i) * heights[i] ;
            st2.emplace(i);

            res = max(res, p1[i] + p2[i] - heights[i]);  // 看p1和p2的状态表示，都包含的 i，要减去重复的一个
        }
        return res;
    }
};

觉得写的不错的话，点个赞吧！~