Ax = b 的迭代解法 —— 共轭梯度 （算法步骤）

线性方程组 Ax =b 除了高斯消元法以外，还有其它的迭代解法，这里我们说的是共轭梯度法。

这里只针对 A 满足 对称 (  ), 正定（即  ），并且是实系数的，那么我们可以用 梯度下降 和 共轭梯度 来解线性方程组 ：

向量  和  是共轭的 （相对于A ）如果满足：

下图两两向量都是针对所在梯度处的矩阵‘共轭’的：

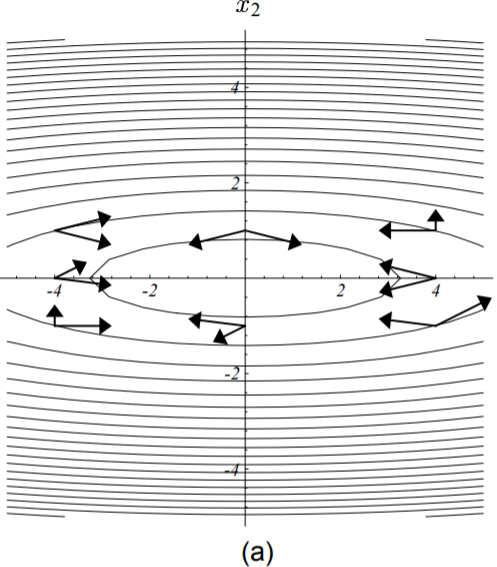
把梯度变换一下，就可以看出‘共轭’其实也就是某种正交：

=============================================

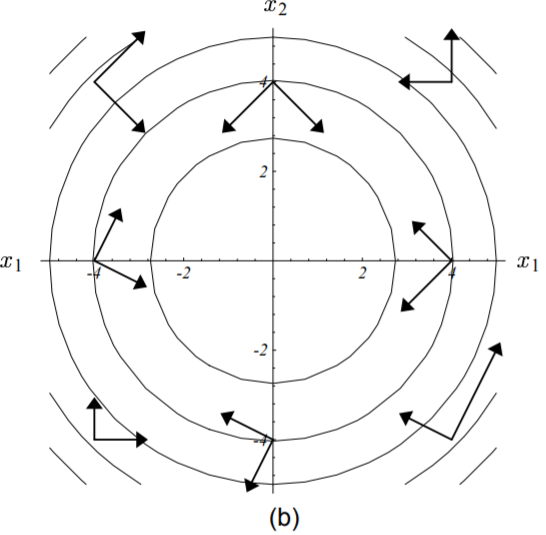
共轭梯度法解：

算法步骤：（from wiki）

---------------------------------------------

python代码：（源于：Baselines：https://github.com/openai/baselines（强化学习算法））

import numpy as np
"""共轭梯度下降"""
def cg(f_Ax, b, cg_iters=10, callback=None, verbose=False, residual_tol=1e-10):
    """
    Demmel p 312
    """
    p = b.copy()
    r = b.copy()
    x = np.zeros_like(b)
    rdotr = r.dot(r)

    fmtstr =  "%10i %10.3g %10.3g"
    titlestr =  "%10s %10s %10s"
    if verbose: print(titlestr % ("iter", "residual norm", "soln norm"))

    for i in range(cg_iters):
        if callback is not None:
            callback(x)
        if verbose: print(fmtstr % (i, rdotr, np.linalg.norm(x)))
        z = f_Ax(p)
        v = rdotr / p.dot(z)
        x += v*p
        r -= v*z
        newrdotr = r.dot(r)
        mu = newrdotr/rdotr
        p = r + mu*p

        rdotr = newrdotr
        if rdotr < residual_tol:
            break

    if callback is not None:
        callback(x)
    if verbose: print(fmtstr % (i+1, rdotr, np.linalg.norm(x)))  # pylint: disable=W0631
    return x

测试代码：

import numpy as np
from gg import cg  #导入 共轭梯度函数 cg

"""
A = np.array([[1.0, 0.0, 0.0],
              [0.0, 1.0, 0.0],
              [0.0, 0.0, 1.0]])
"""
A = np.random.rand(3, 3)  # 保证子行列式均为正
A = np.dot(A.T, A)  # 生成对称矩阵

def f_Ax(p):
    """f_Ax： 输入变量p为列向量，返回变量为矩阵A矩阵乘以向量p"""
    return np.dot(A, p)

x = np.random.rand(3)
b = np.dot(A, x)
print("matrix: \n", A)
print("x: \n", x)
print("b: \n", b)
print("...........................")

print("显示计算过程：")
result = cg(f_Ax, b, verbose=True)
print("matrix A 的特征值：")
print(np.linalg.eig(A)[0])
print("实际x:")
print(x)
print("求得x:")
print(result)

结果：

matrix:
 [[1.33507088 0.69389736 0.579944  ]
 [0.69389736 0.76303172 0.47845562]
 [0.579944   0.47845562 0.41679907]]
x:
 [0.40139385 0.12481318 0.38628268]
b:
 [0.84651911 0.55858167 0.45350579]
...........................
显示计算过程：
      iter residual norm  soln norm
         0       1.23          0
         1   0.000553      0.523
         2   0.000169      0.535
         3   4.11e-28      0.571
matrix A 的特征值：
[2.12734118 0.31861571 0.06894478]
实际x:
[0.40139385 0.12481318 0.38628268]
求得x:
[0.40139385 0.12481318 0.38628268]

=============================================

参考：

https://flat2010.github.io/2018/10/26/%E5%85%B1%E8%BD%AD%E6%A2%AF%E5%BA%A6%E6%B3%95%E9%80%9A%E4%BF%97%E8%AE%B2%E4%B9%89/

图来源：

https://flat2010.github.io/2018/10/26/%E5%85%B1%E8%BD%AD%E6%A2%AF%E5%BA%A6%E6%B3%95%E9%80%9A%E4%BF%97%E8%AE%B2%E4%B9%89/

------------------------------------------------------------------------------