10.1综合强化刷题 Day3 afternoon

　　　　　　　　　　　　　　　　　　　　　　竞赛时间：????年??月??日??:??-??:??

题目名称	a	b	c
名称	a	b	c
输入	a.in	b.in	c.in
输出	a.out	b.out	c.out
每个测试点时限	1s	1s	1s
内存限制	256MB	256MB	256MB
测试点数目	6	100 或 200	10
每个测试点分值	16 或者 17	1 或 0.5	10
是否有部分分	无	无	无
题目类型	传统	传统	传统

a

【问题描述】

你是能看到第一题的 friends 呢。

——hja

给你一个只有小括号和中括号和大括号的括号序列，问该序列是否合法。

【输入格式】

一行一个括号序列。

【输出格式】

如果合法，输出 OK，否则输出 Wrong。

【样例输入】

[(])

【样例输出

Wrong

【数据范围与规定】

对于70%的数据，1 ≤ N≤ 100。

对于100%的数据，1 ≤ N≤ 10000，所有单词由大写字母组成。

简单粗暴的栈模拟

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 10010
using namespace std;
char ch[N];
int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    cin>>ch; int l=strlen(ch);
    ;bool flag=false;
    !=) printf("Wrong");
    else
    {
        ;i<l;i++)
        {
            if(ch[i]=='('||ch[i]=='[') top++;
            else
            {
                if(ch[i]==']')
                {
                    ]=='(') {flag=true; break;}
                    ]=='[') top--;
                }
                else
                {
                    ]=='[') {flag=true; break;}
                    ]=='(') top--;
                }
            }
        }
        if(!flag) printf("OK");
        else printf("Wrong");
    }
    ;
}

AC代码

b

【问题描述】

你是能看到第二题的 friends 呢。

——laekov

Yjq 想要将一个长为l 宽为 w的矩形棺材（棺材表面绝对光滑，所以棺材可以任意的滑动）拖过一个 L 型墓道。

如图所示，L 型墓道两个走廊的宽度分别是a 和 b，呈 90°，并且走廊的长度远大于l 。

现在 Hja 想知道对于给定的 a,b  l, ，最大的 w是多少，如果无论如何棺材都不可能通过，则输出"My poor head =("

【输入格式】

第一行三个用空格分隔的整数a ,  b, l，意义如题目所示。

【输出格式】

输出最大的可能的 w，保留七位小数，如果无论如何棺材都不可能通过，则输出"My poor head =("。

【样例输入 1】

2 2 1

【样例输出 1】

1.0000000

【样例输入 2】

2 2 2

【样例输出 2】

2.0000000

【样例输入 3】

2 2 3

【样例输出 3】

1.3284271

【样例输入 4】

2 2 6

【样例输出 4】

My poor head =(

【数据范围与规定】

对于100%的数据，1 ≤  a, b ,l ≤ 10⁴。

哈哈，只输出没有解的情况能得38.5、、、

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int a,b,l;
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
int main()
{
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
    a=read(),b=read(),l=read();
    printf("My poor head =(");
    ;
}

38.5特判

解析几何+三分求单峰函数最值

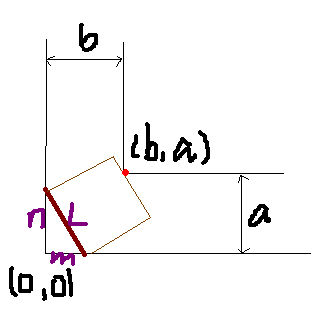
设直线解析式为 y=（-n/m）* x+n

整理，得：n * x + m * y - n * m = 0

点（b，a）到直线的距离为：|  b * n + a * m - n * m | / L

(L : 根号下（n^2 + m^2）=L)

//特判三种情况，一种是怎么找都能拖过去的（w最大等于l），一种是可以横着过去的（w要比b小才能过去），一种是可以竖着过去的（w要比a小才能过去）
//进行三分找最优解
//对于这个棺材我们可以知道解析式为n*x+m*y-n*m=0，(b,a)这个点到直线的距离为|n*b+m*a-n*m|/l
//我们知道我们要使棺材能过去，必须要是他在任何地方都能过去，也就是说这个棺材的w要比这个点到直线的距离的最小值小或者等于
//这样的话，我们就转换成单峰函数求最值，采用三分法
//三分法？三分法的思路与二分法很类似，不过其用途没有那么广泛，主要用于求单峰函数的极值。
while(t<100)//对于实数类型的三分或二分直接分100次就够了

//当最小值为负数的时候即为无论怎样都过不去的时候，直接输出My poor head =(

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int a,b,l,t;
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
double work(double n)
{
    double m=sqrt(1.0*l*l-n*n);
    return (m*a+b*n-n*m)/l;//求出点到直线的距离
}
int main()
{
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
    a=read(),b=read(),l=read();
    ;}
    ;}
    ;}
    //特判三种情况，一种是怎么找都能拖过去的（w最大等于l），一种是可以横着过去的（w要比b小才能过去），一种是可以竖着过去的（w要比a小才能过去）
    ,R=l,ans=-1e8,mid1,mid2,t1,t2;
    //进行三分找最优解
    //对于这个棺材我们可以知道解析式为n*x+m*y-n*m=0，(b,a)这个点到直线的距离为|n*b+m*a-n*m|/l
    //我们知道我们要使棺材能过去，必须要是他在任何地方都能过去，也就是说这个棺材的w要比这个点到直线的距离的最小值小或者等于
    //这样的话，我们就转换成单峰函数求最值，采用三分法
    //三分法？三分法的思路与二分法很类似，不过其用途没有那么广泛，主要用于求单峰函数的极值。
    )//对于实数类型的三分或二分直接分100次就够了
    {
        t++;
        mid1=(R-L)/+L,mid2=R+L-mid1;//三分
        t1=work(mid1),t2=work(mid2);
        ||t2<) {printf(;}//当最小值为负数的时候即为无论怎样都过不去的时候
        if(t1<t2) ans=t1,R=mid2;
        else ans=t2,L=mid1;
    }
    printf("%.7lf",ans);
    ;
}

AC代码

c

【问题描述】

你是能看到第三题的 friends 呢。

——aoao

树是个好东西，删掉树一条边要 1 的代价，随便再加一条边有 1 的代价，求最小的代价把树变成环。

【输入格式】

第一行一个整数N，代表树的点数。

接下来 N− 1行，每行两个数代表树的一条边。

【输出格式】

一行一个整数代表答案。

【样例输入】

4

1 2

2 3

2 4

【样例输出】

3

【数据规模与约定】

对于30%的数据，1 ≤ N≤ 10。

对于60%的数据，1 ≤N ≤ 1000。

对于100%的数据，1 ≤ N≤ 100000。

明明写了个60分的部分分，结果node结构体里面的数不知道怎么改，弄出负数来了，然后就只得了30分

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 1010
using namespace std;
int n,x,y,s,in[N],sum,ans,q[N][N];
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
struct Node
{
    int num,w,s;
}node[N][N];
int cmp(Node a,Node b){return a.w>b.w;}
int main()
{
//    freopen("c.in","r",stdin);
//    freopen("c.out","w",stdout);
    n=read();
    ;i<n;i++)
    {
        x=read(),y=read();
        in[x]++,in[y]++;
        q[x][in[x]]=y;
        q[y][in[y]]=x;
    }
    ;i<=n;i++)
      ;j<=in[i];j++)
        node[i][j].num=q[i][j],node[i][j].w=in[q[i][j]],node[i][q[i][j]].s=j;
    ;i<=n;i++)
     )
     {
        ;j<=in[i];j++)
        {
            y=node[i][j].num;
            node[y][node[y][i].s].w=;
        //    node[y][node[y][i].s].num;
        }
        sort(node[i]+,node[i]++in[i],cmp);
        sum=,,s=;
         while(sum)
         {
             y=node[i][s].num,in[y]--;
            ;j<=;j++)
            {
                x=node[y][j].num;
                node[x][node[x][y].s].w--;
            }
             ans+=,sum--,s++;
         }
     }
    ;i<=n;i++) printf("%d ",in[i]);
    ans+=*n;sum=;
    ;i<=n;i++)
     sum+=in[i];
    ans-=sum;ans/=;
    printf("\n%d",ans);
    ;
}

30分代码

正解树形dp，刘大佬用乱搞A掉的，由于本蒟蒻不会dp，所以听的乱搞的思路

我们先把原来的树变成一条链，然后变成链的代价+1以后就是总代价。怎样求变成链的代价呢？我们搜索整棵树，我们随便找一个入度为1的节点为根节点，然后搜索整棵树，当一个节点的度数>2的时候，我们就要对其进行删边，删去除那两条边以外的边由于我们要变成一条链，因此我们在删完边以后还要在建相同数量的边（原树的边的条数为n-1，链的条数也为n-1）因此我们这个地方要乘2，我们把这条边删去，那么他的父亲节点的入读就-1

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 100010
using namespace std;
];
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
struct Edge
{
    int to,next,from;
}edge[N<<];
int add(int x,int y)
{
    tot++;
    edge[tot].to=y;
    edge[tot].next=head[x];
    head[x]=tot;
}
void dfs(int x,int fa)
{
    for(int i=head[x];i;i=edge[i].next)
    {
        int t=edge[i].to;
        if(t==fa) continue;
        dfs(t,x);
        )
        {
            in[x]--;
            ans+=()*;
        }
    }
}
int main()
{
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
    n=read();
    ;i<n;i++)
    {
        x=read(),y=read();
        add(x,y),add(y,x);
        in[x]++,in[y]++;
    }
    ;i<=n;i++)
      ) {root=i; break;}
    dfs(root,-);
    printf();
    ;
 } 

AC代码

　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　距 NOIp2017 还剩 28 天

　　                             你可以做的事情还有很多，即使到最后一秒也不要放弃，因为不到结束的那一刻谁也不知道结果会怎样。