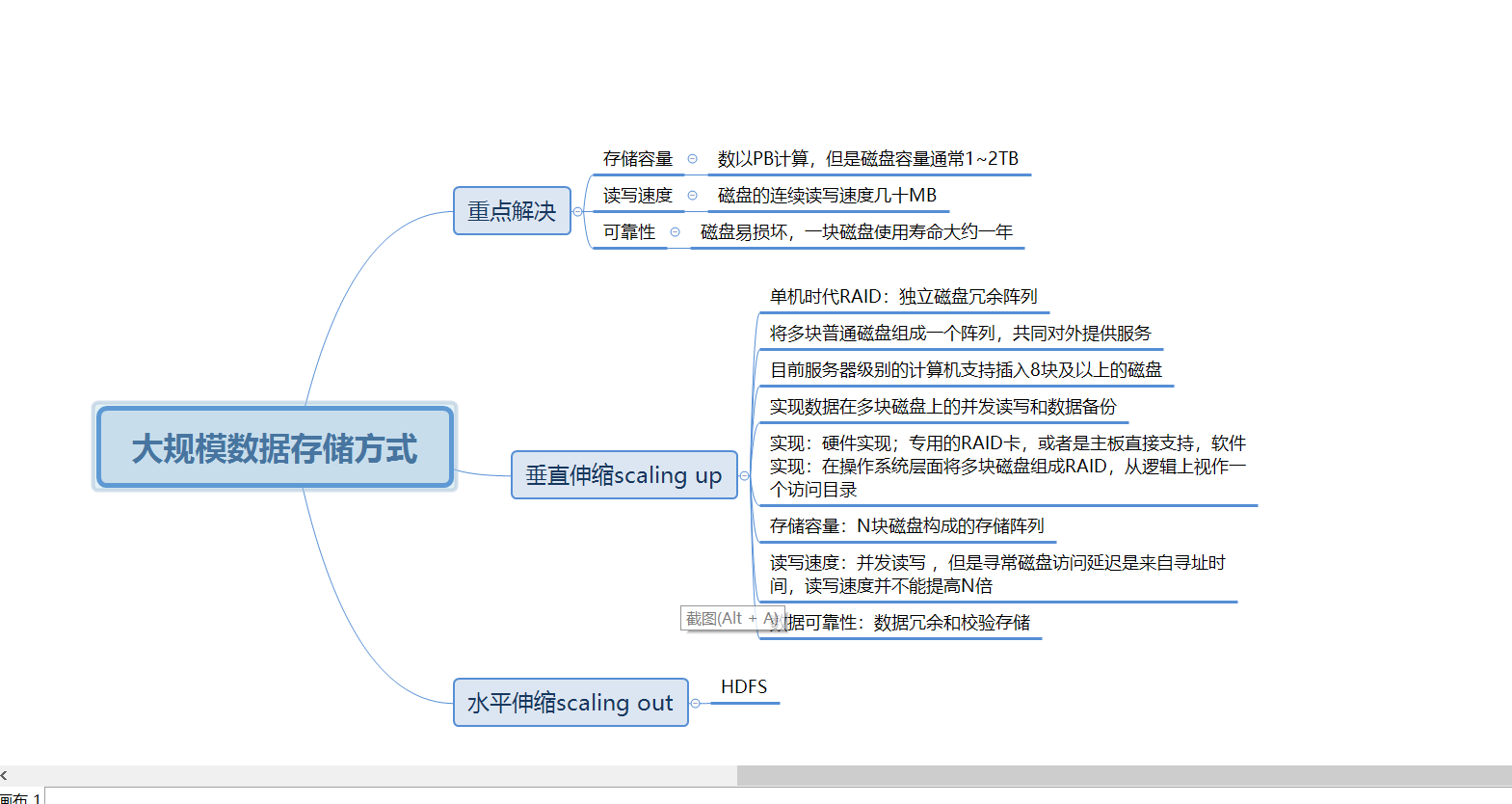
从RAID看垂直伸缩到水平伸缩的演化
磁盘的读写过程,最消耗时间的地方就是在磁盘中磁道寻址的过程,而一旦寻址完成,写入数据的速度很快。
连续写入:写入只寻址一次 存储位置与逻辑位置相邻 不用多次寻址
随机写入:每写一次 便寻址一次 增加了磁盘的寻址时间
因为b+树的节点包含多个信息,可以连续读写磁盘

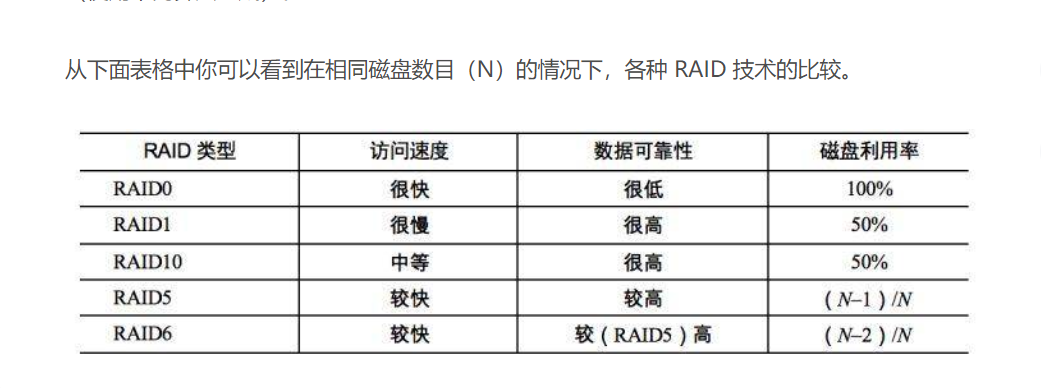
RAID 0
数据分成N份,同时写入N块磁盘,数据整体写入速度快N倍,较快的读写速度,但是没有做数据备份,所以磁盘损坏之后数据完整性被破坏。
RAID1
一份数据同时写如两块磁盘,具有极高可靠性
RAID10
所有磁盘N平分成两份,数据同时在两份磁盘写入,磁盘利用率低,有一半的磁盘用来写入备份数据;
RAID3
将数据分成N-1份,并发写入N-1块磁盘,在第N块磁盘记录校验数据;这样其他任何一块磁盘损坏(包括校验盘),否可以利用其他N-1块磁盘修复;
缺点:在数据修改较多的场景,任何磁盘的修改都会导致第N块磁盘的重写校验数据,第N块磁盘经常更换,所以在日常中很少使用此种模式
RAID5
3的进阶,校验数据不是写在第N块磁盘,而是螺旋式的写入N块磁盘中,校验数据的修改平均到所有磁盘上,避免一块磁盘的频繁损坏现象
RAID6
使用场景:数据需要很高的可靠性,在同时出现两块磁盘损坏的情况下,仍然需要修复修复数据
数据写入N-2块磁盘,并在剩余两块磁盘中螺旋式的写入校验信息(使用不同算法生成)
从RAID看垂直伸缩到水平伸缩的演化的更多相关文章
- k8s Pod的自动水平伸缩(HPA)
我们知道,当访问量或资源需求过高时,使用:kubectl scale命令可以实现对pod的快速伸缩功能 但是我们平时工作中我们并不能提前预知访问量有多少,资源需求多少. 这就很麻烦了,总不能为了需求总 ...
- MySQL垂直拆分和水平拆分的优缺点和共同点总结
数据的拆分(Sharding)根据其拆分分规则的类型,可以分为两种拆分模式.一种是按照不同的表(或者Schema)来切分到不同的数据库(主机)之上,这种切可以称之为数据的垂直(纵向)拆分:另外一种则是 ...
- 数据库垂直拆分,水平拆分利器,cobar升级版mycat(转)
原文:数据库垂直拆分,水平拆分利器,cobar升级版mycat 1,关于Mycat Mycat情报 基于阿里的开源cobar ,可以用于生产系统中,目前在做如下的一些改进: 非阻塞IO的实现,相对于目 ...
- SilverLight:布局(2)GridSplitter(网格分割)垂直分割、水平分割
ylbtech-SilverLight-Layout: 布局(2)GridSplitter(网格分割)垂直分割.水平分割 A, Splitter(分割)对象之 GridSplitter(网格分割)1: ...
- kubernetes 水平伸缩及yaml格式编写
Replication Controller:用来部署.升级PodReplica Set:下一代的Replication ControllerDeployment:可以更加方便的管理Pod和Repli ...
- css实现水平伸缩菜单
ul li a{transition:width 500ms ease;} a:hover{width:*;} 高度向上延伸用height:*;margin-top:-*px;//负值实现向上
- js实现水平伸缩菜单
window.onload=function(){ var aA=document.getElementsByTagName('a'); for(var i=0; i<aA.length; i+ ...
- FineUI第十四天---布局之垂直布局和水平布局
布局值水平布局和垂直布局 垂直盒子布局和水平盒子布局非常灵活易用,在很大程度上能够取代锚点布局,行布局和列布局. 1.垂直盒子布局: BoxConfigAlign:控制子容器的的尺寸 Start:位于 ...
- java中向JTextArea中添加滚动条(垂直的和水平的)
这次在研究java的swing类时,在做一个实例时,发现了JTextArea中添加滚动条的问题,经过网上查找资料和自己测试发现有以下用法: 1.首先应该把JTextArea添加到一个JScrollPa ...
随机推荐
- 超限学习机 (Extreme Learning Machine, ELM) 学习笔记 (一)
1. ELM 是什么 ELM的个人理解: 单隐层的前馈人工神经网络,特别之处在于训练权值的算法: 在单隐层的前馈神经网络中,输入层到隐藏层的权值根据某种分布随机赋予,当我们有了输入层到隐藏层的权值之后 ...
- ajax进度条
.graph { width: 400px; height: 25px; border: 1px solid #f8b3d0; } .bar { background-color: #ffe7f4; ...
- 如何让你的手机U盘集PE工具、系统安装、无线破解等众多功能于一身
不久前,手里的U盘坏了,于是乎,又在网上淘了一个Type-C U盘,刚好手机电脑都可以用. 那么现在U有了,我们要做什么呢? 第一:让U盘插在手机上时,可以供手机读写,实现手机存储扩容,随插随用,简单 ...
- MysqL的root用户不允许远程连接,只能通过PHPMYADMIN
解决方法:1.改表法 可能是你的帐号不允许从远程登陆,只能在localhost.这个时候只要在localhost的那台电脑,登入mysql后,更改 "mysql" 数据库里的 &q ...
- 简单的可兼容所有浏览器的操作html元素的javascript框架
1.根据id名称取元素 $id(idName) 2.根据class定义取元素 $class(className)返回所有class被定义成className的元素数组,或者$Eclass(clas ...
- BZOJ 1370 [Baltic2003]Gang团伙:并查集【虚点】
题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=1370 题意: 在某城市里住着n个人,任何两个认识的人不是朋友就是敌人,而且满足: (1)我 ...
- laravel基础课程---4、Laravel基础网站结构搭建
laravel基础课程---4.Laravel基础网站结构搭建 一.总结 一句话总结: 1.搭建网站前后台路由:在路由组Route::group()中设置好命名空间和前缀 2.搭建控制器:比如1)新建 ...
- jQuery bootstrap框架下重置下拉框选择
前端页面中下拉选择框采用bootstrap-select美化,如下图:
- Spring笔记03(Spring创建对象的三种方式)
1.创建对象的三种方式和bean的生命周期的验证: Animal接口代码: package cn.pb.dao; /** * 动物接口 */ public interface Animal { //吃 ...
- poj2823Sliding Window——单调队列
题目:http://poj.org/problem?id=2823 单调队列模板. 代码如下: #include<iostream> #include<cstdio> usin ...
