BZOJ1491 [NOI2007]社交网络【floyd】

题目

在社交网络（socialnetwork）的研究中，我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题。

在一个社交圈子里有n个人，人与人之间有不同程度的关系。我们将这个关系网络对应到一个n个结点的无向图上，

两个不同的人若互相认识，则在他们对应的结点之间连接一条无向边，并附上一个正数权值c，c越小，表示两个人

之间的关系越密切。我们可以用对应结点之间的最短路长度来衡量两个人s和t之间的关系密切程度，注意到最短路

径上的其他结点为s和t的联系提供了某种便利，即这些结点对于s和t之间的联系有一定的重要程度。我们可以通过

统计经过一个结点v的最短路径的数目来衡量该结点在社交网络中的重要程度。考虑到两个结点A和B之间可能会有

多条最短路径。我们修改重要程度的定义如下：令Cs,t表示从s到t的不同的最短路的数目，Cs,t(v)表示经过v从s

到t的最短路的数目；则定义

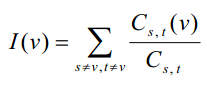
为结点v在社交网络中的重要程度。为了使I(v)和Cs,t(v)有意义，我们规定需要处理的社交网络都是连通的无向图

，即任意两个结点之间都有一条有限长度的最短路径。现在给出这样一幅描述社交网络的加权无向图，请你求出每

一个结点的重要程度。

输入格式

输入第一行有两个整数n和m，表示社交网络中结点和无向边的数目。在无向图中，我们将所有结点从1到n进行编号

。接下来m行，每行用三个整数a，b，c描述一条连接结点a和b，权值为c的无向边。注意任意两个结点之间最多有

一条无向边相连，无向图中也不会出现自环（即不存在一条无向边的两个端点是相同的结点）。n≤100；m≤4500

，任意一条边的权值 c 是正整数，满足：1≤c≤1000。所有数据中保证给出的无向图连通，且任意两个结点之间

的最短路径数目不超过 10^10

输出格式

输出包括n行，每行一个实数，精确到小数点后3位。第i行的实数表示结点i在社交网络中的重要程度。

输入样例

4 4

1 2 1

2 3 1

3 4 1

4 1 1

输出样例

1.000

提示

社交网络如下图所示。

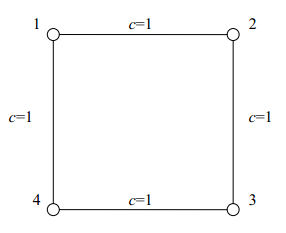
对于 1 号结点而言，只有 2 号到 4 号结点和 4 号到 2 号结点的最短路经过 1 号结点，而 2 号结点和 4 号结

点之间的最短路又有 2 条。因而根据定义，1 号结点的重要程度计算为 1/2 + 1/2 = 1 。由于图的对称性，其他

三个结点的重要程度也都是 1 。

题解

n很小，立刻想到floyd

跑一遍可以求出最短路及路径数

跑第二次可以更新中介点的答案

#include<iostream>

#include<cmath>

#include<cstdio>

#include<cstring>

#include<algorithm>

#define LL long long int

#define REP(i,n) for (int i = 1; i <= (n); i++)

#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)

#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");

using namespace std;

const int maxn = 105,maxm = 100005,INF = 1000000000;

inline int read(){

	int out = 0,flag = 1; char c = getchar();

	while (c < 48 || c > 57) {if (c == '-') flag = -1; c = getchar();}

	while (c >= 48 && c <= 57) {out = (out << 3) + (out << 1) + c - '0'; c = getchar();}

	return out * flag;

}

double d[maxn][maxn],cnt[maxn][maxn],f[maxn];

int n,m;

void floyd(){

	REP(k,n) REP(i,n) REP(j,n){

		if (i == k || i == j || k == j) continue;

		if (d[i][k] + d[j][k] < d[i][j])

			d[i][j] = d[i][k] + d[k][j],cnt[i][j] = cnt[i][k] * cnt[k][j];

		else if (d[i][k] + d[k][j] == d[i][j])

			cnt[i][j] += cnt[i][k] * cnt[k][j];

	}

	REP(k,n) REP(i,n) REP(j,n){

		if (i == k || i == j || k == j) continue;

		if (d[i][k] + d[k][j] == d[i][j])

			f[k] += cnt[i][k] * cnt[k][j] / cnt[i][j];

	}

}

int main(){

	n = read(); m = read(); int a,b,v;

	fill(d[0],d[0] + maxn * maxn,INF);

	REP(i,n) d[i][i] = 0;

	while (m--){

		a = read(); b = read(); v = read();

		d[a][b] = d[b][a] = v; cnt[a][b] = cnt[b][a] = 1;

	}

	floyd();

	REP(i,n) printf("%.3lf\n",f[i]);

	return 0;

}