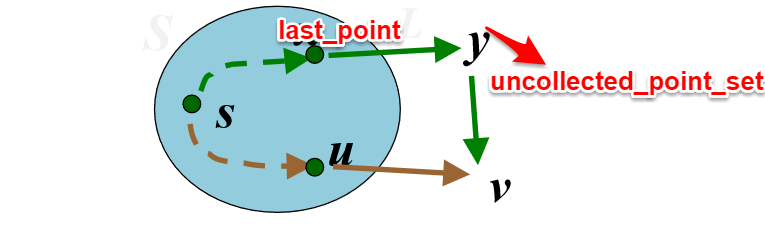
Dijkstra算法正确性证明

Dijkstra算法正确性证明的更多相关文章
- 互联网IP合全局路由优化的原则-Dijkstra算法证明
周末继续写东西的一半填补了,为了达到完美的一天.我们知道一个事实,IP地址太多.统一管理是不可能的了,无论从控制平面从数据/管理层表示,飞机是如此. 所以.IP协议被设计为可伸缩.供IP路由术语,跳路 ...
- 求两点之间最短路径-Dijkstra算法
Dijkstra算法 1.定义概览 Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径.主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止.D ...
- Dijkstra算法优先队列实现与Bellman_Ford队列实现的理解
/* Dijkstra算法用优先队列来实现,实现了每一条边最多遍历一次. 要知道,我们从队列头部找到的都是到 已经"建好树"的最短距离以及该节点编号, 并由该节点去更新 树根 到其 ...
- 关于dijkstra算法的一点理解
最近在准备ccf,各种补算法,图的算法基本差不多看了一遍.今天看的是Dijkstra算法,这个算法有点难理解,如果不深入想的话想要搞明白还是不容易的.弄了一个晚自习,先看书大致明白了原理,就根据书上的 ...
- 最短路模板(Dijkstra & Dijkstra算法+堆优化 & bellman_ford & 单源最短路SPFA)
关于几个的区别和联系:http://www.cnblogs.com/zswbky/p/5432353.html d.每组的第一行是三个整数T,S和D,表示有T条路,和草儿家相邻的城市的有S个(草儿家到 ...
- Dijkstra算法(二)之 C++详解
本章是迪杰斯特拉算法的C++实现. 目录 1. 迪杰斯特拉算法介绍 2. 迪杰斯特拉算法图解 3. 迪杰斯特拉算法的代码说明 4. 迪杰斯特拉算法的源码 转载请注明出处:http://www.cnbl ...
- Dijkstra算法(一)之 C语言详解
本章介绍迪杰斯特拉算法.和以往一样,本文会先对迪杰斯特拉算法的理论论知识进行介绍,然后给出C语言的实现.后续再分别给出C++和Java版本的实现. 目录 1. 迪杰斯特拉算法介绍 2. 迪杰斯特拉算法 ...
- 最短路问题Dijkstra算法
Dijkstra算法可以解决源点到任意点的最短距离并输出最短路径 准备: 建立一个距离数组d[ n ],记录每个点到源点的距离是多少 建立一个访问数组v[ n ],记录每个点是否被访问到 建立一个祖先 ...
- dijkstra算法求最短路
艾兹格·W·迪科斯彻 (Edsger Wybe Dijkstra,1930年5月11日~2002年8月6日)荷兰人. 计算机科学家,毕业就职于荷兰Leiden大学,早年钻研物理及数学,而后转为计算学. ...
随机推荐
- 二、HTTP请求
一.测试对象:v2ex的api 文档:https:www.v2ex.com/p/7vpTEc53 api:https://www.v2ex.com/api/topic/hot.json 最热主题:相当 ...
- 基于ZooKeeper实现简单的服务注册于发现
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明.本文链接:https://blog.csdn.net/Shaun_luotao/article/ ...
- linux安装6.5.3版本elastic search
到官网https://www.elastic.co/cn/downloads/elasticsearch下载压缩包,目前最新的版本是7.3.2,我想下6.5.3,点击下面的past release链接 ...
- 泡泡一分钟:Topomap: Topological Mapping and Navigation Based on Visual SLAM Maps
Topomap: Topological Mapping and Navigation Based on Visual SLAM Maps Fabian Bl¨ochliger, Marius Feh ...
- Spring cloud微服务安全实战_汇总
Spring cloud微服务安全实战 https://coding.imooc.com/class/chapter/379.html#Anchor Spring Cloud微服务安全实战-1-1 课 ...
- Spring Cloud Eureka 服务发现 4.2
在微服务架构中,服务发现可以说是最为核心和基础的模块,该模块主要用于实现各个微服务实例的自动化注册与发现.在Spring Cloud的子项目中,Spring Cloud Netflix提供了Eur ...
- spring AOP的基本概念
AOP的概念和使用原因 现实中有一些内容并不是面向对象(OOP)可以解决的,比如数据库事务,它对于企业级的Java EE应用而言是十分重要的,又如在电商网站购物需要经过交易系统.财务系统,对于交易系统 ...
- 【JQuery插件】元素根据滚动条位置自定义吸顶效果
;(function($){ $.fn.extend({ /* 元素根据滚动条位置自定义吸顶插件 @defaultTop 初始化top位置 @startTop 开始滚动和回复原样的位置 @demo v ...
- 常见浏览器CSS hack方法总结
ie6和ie7 #tip {*background:black; /*IE7 背景变黑色*/_background:orange; /*IE6 背景变橘色*/} IE8和IE9 :root .test ...
- golang中sync.RWMutex和sync.Mutex区别
golang中sync包实现了两种锁Mutex (互斥锁)和RWMutex(读写锁),其中RWMutex是基于Mutex实现的,只读锁的实现使用类似引用计数器的功能. type Mutex f ...
