python实现迭代法求方程组的根

有方程组如下：

迭代法求解x，python代码如下：

import numpy as np
import matplotlib.pyplot as plt

A = np.array([[8, -3, 2], [4, 11, -1], [6, 3, 12]])
b = np.array([[20, 33, 36]])

# 方法一：消元法求解方程组的解
result = np.linalg.solve(A, b.T)
# print('Result:\n', result)

# 方法二：迭代法求解方程组的解
B = np.array([[0, 3/8, -2/8], [-4/11, 0, 1/11], [-6/12, -3/12, 0]])
f = np.array([[20/8, 33/11, 36/12]])
error = 1.0e-6
steps = 100
xk = np.zeros((3, 1))  # initialize parameter setting
errorlist = []
for k in range(steps):
    xk_1 = xk
    xk = np.matmul(B, xk) + f.T
    print('xk:\n', xk)
    errorlist.append(np.linalg.norm(xk-xk_1))
    if errorlist[-1] < error:
        print('iteration: ', k+1)
        break

# 把误差画出来
x_axis = [i for i in range(len(errorlist))]
plt.figure()
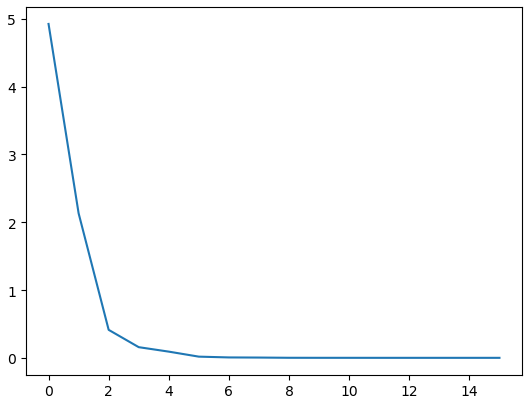
plt.plot(x_axis, errorlist)

结果如下：

【参考文献】

《机器学习算法原理与编程实践》郑捷，第五章第一节