【bfs分层图 dp】hihocoder#1147 : 时空阵

最短路径树上分层dp的一类套路吧

题目大意

幽香这几天学习了魔法，准备建造一个大型的时空传送阵。

幽香现在可以在幻想乡的n个地点建造一些传送门，如果她建造了从地点a与地点b之间的传送门，那么从a到b和从b到a都只需要单位1的时间。

同时这些地点之间在地理上是非常遥远的，因此来往他们必须使用传送门。

现在幽香想要问你，有多少种建造传送门的方案，使得地点1和地点n之间的最短距离恰好为k？两个方案不同当且仅当建造的传送门的集合不同。不能建造节点到自身的传送门，两个点之间也最多造一个传送门。

$n,k \le 100$

---

题目分析

特殊性质在于每条边长度都为1，这点让人联想到bfs；而看到最短路则自然想起最短路径树。

那么我们就考虑按照bfs序dp这张图的最短路径树，也就是分层往下dp。在分层dp的树中，跨层的点不能连边；邻层及同层的点可以随意连边，最终目标是把$n$号点安排在$k+1$层，如果还有剩下的点则接下去随意安排。

不过这里有一种省去分类讨论的小trick：我们不计标号地计算剩下$n-1$个点的方案数，而由于这$n-1$个点是完全等价的，相当于最后再把总方案数乘以$(n-1)^{-1}$即可。

用$f_{i,t,l}$表示构造了$i$层，总共使用了$t$个节点（包括1号点），当前层有$l$个节点的方案数。转移时枚举上一层有$p$个节点。边界条件$f_{1,1,1}=1$

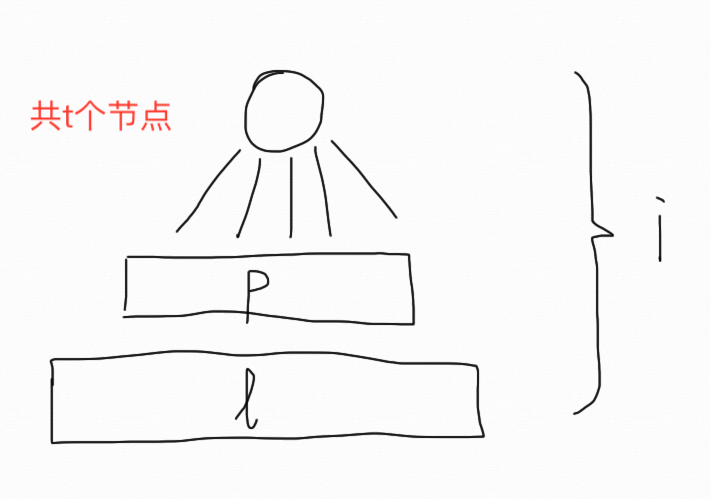
大致形状如上所示。

考虑p到l的转移：首先从$n-(t-l)$个点中取出$l$个点，取出的每个点向$p$个点连边有$2^p-1$种方案；$l$个点同层连边有$2^{l\choose 2}$种方案。

最后再枚举所有情况统计一趟即可。

 #include<bits/stdc++.h>
 #define MO 1000000007
 typedef long long ll;
 const int maxn = ;

 int n,k,fac[maxn],facinv[maxn],mi[maxn];
 ll f[maxn][maxn][maxn],ans;

 int qmi(ll a, ll b)
 {
     int ret = ;
     for (a%=MO; b; b>>=,a=1ll*a*a%MO)
         if (b&) ret = 1ll*ret*a%MO;
     return ret;
 }
 int C(int n, int m)
 {
     if (n < m) return ;
     return 1ll*fac[n]*facinv[n-m]%MO*facinv[m]%MO;
 }
 int main()
 {
     scanf("%d%d",&n,&k);
     facinv[] = facinv[] = fac[] = mi[] = ;
     for (int i=; i<=; i++)
         facinv[i] = MO-1ll*MO/i*facinv[MO%i]%MO;
     for (int i=; i<=; i++)
         mi[i] = 2ll*mi[i-]%MO, fac[i] = 1ll*fac[i-]*i%MO, facinv[i] = 1ll*facinv[i-]*facinv[i]%MO;
     f[][][] = ;
     for (int i=; i<=k+; i++)
         for (int t=i; t<=n; t++)
             for (int l=; l<=t-i+; l++)
                 for (int p=; p<=t-l-i+; p++)
                     f[i][t][l] = (f[i][t][l]+1ll*f[i-][t-l][p]*qmi(mi[p]-, l)%MO*C(n-t+l, l)%MO*qmi(, C(l, ))%MO)%MO;
     for (int i=; i<=n; i++)
         for (int j=; j<=n; j++)
             if (f[k+][i][j])
                 ans = (ans+1ll*f[k+][i][j]*j%MO*qmi(, C(n-i, ))%MO*qmi(, 1ll*j*(n-i)%MO))%MO;
     printf("%lld\n",1ll*ans*qmi(n-, MO-)%MO);
     return ;
 }

END