Andrew算法求二维凸包-学习笔记

凸包的概念

首先，引入凸包的概念：

（有点窄的时候...图片右边可能会被吞，拉开图片看就可以了）

大概长这个样子：

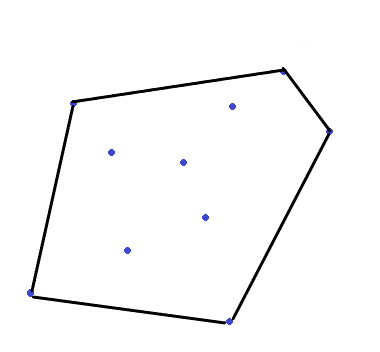
那么，给定一些散点，如何快速地求出凸包呢（用在凸包上的点来表示凸包）

Andrew算法流程和思想

常见的求凸包的算法有$Graham$和$Andrew$，$Andrew$是$Graham$扫描算法的变种，和$Graham$相比，$Andrew$更快，且更稳定，所以主要讲一下$Andrew$。

首先把所有点以$x$坐标为第一关键字，$y$坐标为第二关键字从小到大进行排序，可以肯定第一个点和最后一个点在答案中。

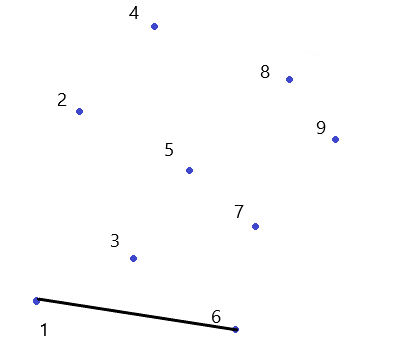
接下来用以下的例子来帮助理解算法流程：

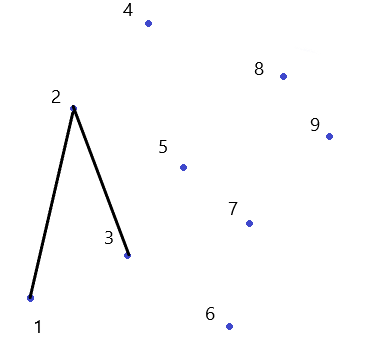
第一次，把$1$和$2$加入答案中

尝试把$3$加进去，发现凹进去了，所以把$2$丢掉，把$3$放进去

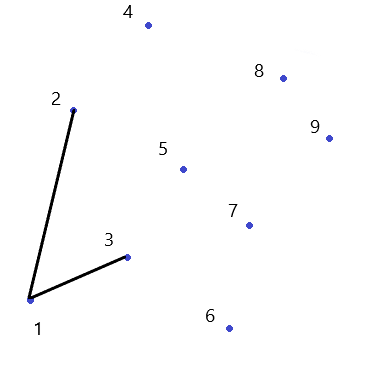
我们来看看$2$被丢掉，$3$成功上位的原因（凹进去的原因）：
发现是斜率（或者...可以总结成叉积？

在下图中$1->2$的斜率大于$1->3$的斜率，又因为之前按$x$递增排序，所以可以说明$2$在$3$的左上，所以是凹进去的。

换句话说，如果加进去这个点（即当前点，记为$i$）和$i-2$号点的斜率小于$i$号点和$i-1$号点的斜率，那么就要把$i-1$号点去掉并加入$i$号点来维护凸包的性质（不让它凹进去）

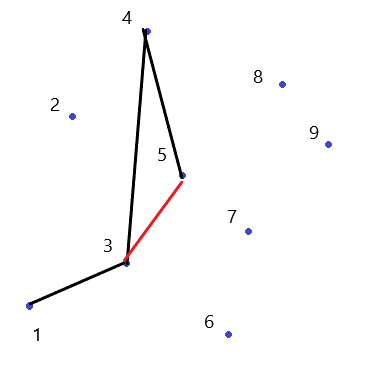
接下来加入$4$，$1->4$斜率大于$1->3$斜率，所以$3$不用被丢掉。

加入$5$，$3->5$斜率小于$3->4$斜率，所以丢掉$4$，加入$5$

加入$6$，一样的理由，一样的操作。（$3->6$斜率小于$3->5$斜率，丢掉$5$，加入$6$）

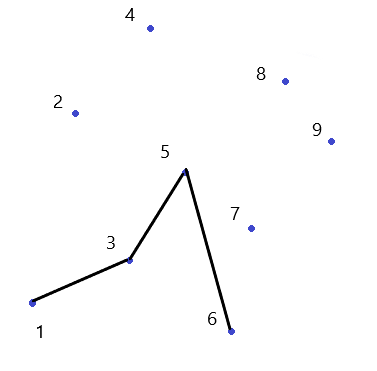
然后发现$3$那个地方也凹进去了（$1->6$的斜率小于$1->3$的斜率）

所以$3$也要被丢掉，然后只剩下两个点：

（所以写代码的时候要用$while$）

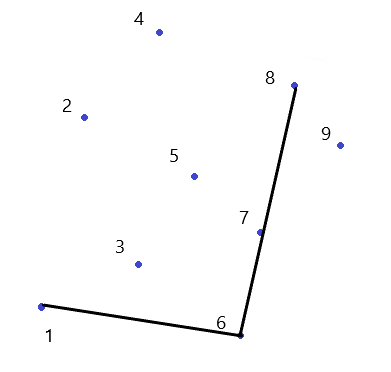
接着来，加入$7$:

然后是$8$，发现...斜率只小一点点（图没画好，这刁钻的角度，将就看一下吧...），所以$7$要删掉

不过也顺便解决一个共线的问题，共线嘛，很好解决，反正两个点都在凸包上，都不丢就可以了，后面如果那一条线不属于凸包的话，用$while$丢点的时候两个点斜率是一样的，总会被丢出去的。

然后是$9$，发现斜率小，所以丢掉$8$：

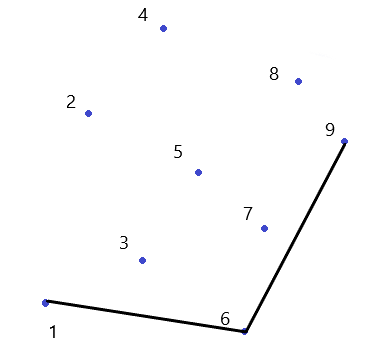
啊哈，然后发现所有点都已经遍历完了，成功达到了$9$，可是凸包还有一半呢。

倒着再来一次就可以求出上面那个盖盖了：

（下面放流程图，不一一解说了（好累），操作是一样的）

（把$7$悄悄地挪了一下位置）

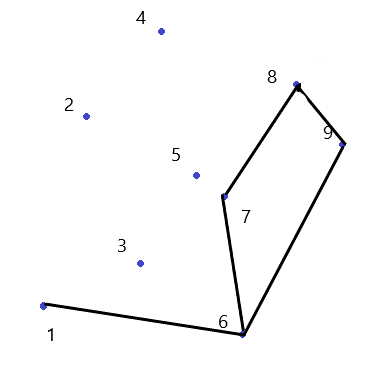
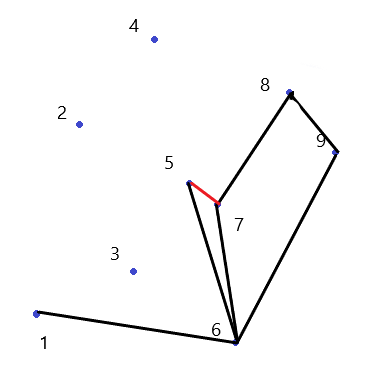
（丢掉$6$，发现斜率的关系和正着的那一次都一样，都是小于）

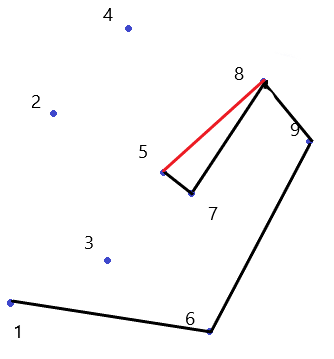
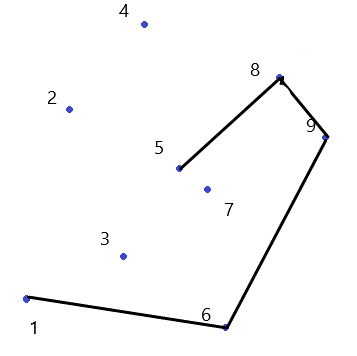
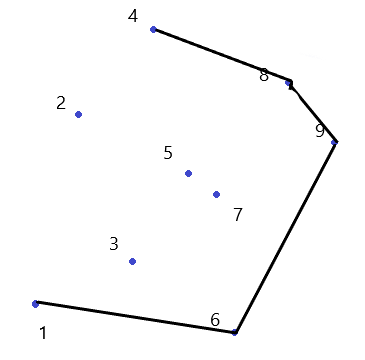
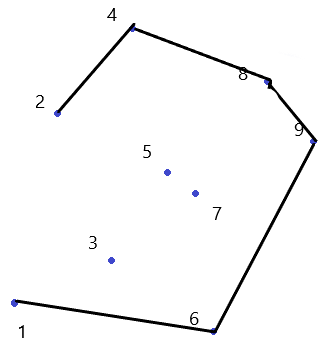
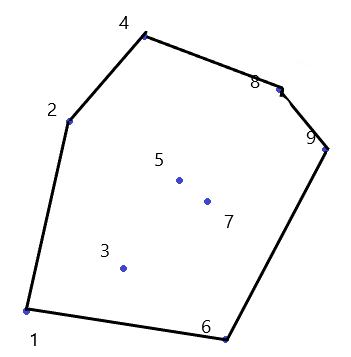
这样， 凸包就求出来啦！

按照以上的思路写代码就可以啦。

例题& 板子

例题： 求凸包的周长：

 /*
 ID: Starry21
 LANG: C++
 TASK: fc
 */
 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #include<cstring>
 #include<queue>
 #include<map>
 #include<iostream>
 #include<cmath>
 using namespace std;
 #define ll long long
 #define INF 0x3f3f3f3f
 #define N 10005
 struct node{
     double x,y;
 };
 node p[N],s[N]/*凸包上的点*/;
 int n;
 double dis(node a,node b)
 {
     return sqrt(((a.x-b.x)*(a.x-b.x))+((a.y-b.y)*(a.y-b.y)));
 }
 bool cmp(node a,node b)
 {
     if(a.x==b.x) return a.y<b.y;
     return a.x<b.x;
 }
 double getk(node a,node b)
 {
     if(a.x==b.x) return INF;//在一条竖线上 斜率看成无限大
     return (b.y-a.y)/(b.x-a.x);
 }
 double Andrew()
 {
     sort(p+,p+n+,cmp);
     int cnt=,tot=;
     double sum=0.0;
     for(int i=;i<=n;i++)
     {
         s[++cnt]=p[i];
         while(cnt>=&&getk(s[cnt-],s[cnt])<getk(s[cnt-],s[cnt-]))
             s[cnt-]=s[cnt],cnt--;
     }
     for(int i=;i<=cnt-;i++)
         sum+=dis(s[i],s[i+]);
     tot=cnt;
     cnt=;
     for(int i=n;i>=;i--)
     {
         s[++cnt]=p[i];
         while(cnt>=&&getk(s[cnt-],s[cnt])<getk(s[cnt-],s[cnt-]))
             s[cnt-]=s[cnt],cnt--;
     }
     for(int i=;i<=cnt-;i++)
         sum+=dis(s[i],s[i+]);
     tot+=cnt;
     tot-=;//tot是凸包上点的个数
     //printf("%d\n",tot);
     return sum;
 }
 int main()
 {
     //freopen("fc.in","r",stdin);
     //freopen("fc.out","w",stdout);
     scanf("%d",&n);
     for(int i=;i<=n;i++)
         scanf("%lf %lf",&p[i].x,&p[i].y);
     printf("%.2lf\n",Andrew());
     return ;
 }

Code

还有一个用叉积写的，原理都是一样的， 不过我自己不是很喜欢这种写法：

 /*
 ID: Starry21
 LANG: C++
 TASK: shuttle
 */
 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #include<cstring>
 #include<queue>
 #include<map>
 #include<iostream>
 #include<cmath>
 using namespace std;
 #define ll long long
 #define INF 0x3f3f3f3f
 #define N 10005
 struct node{
     double x,y;
 };
 node p[N],s[N]/*凸包上的点*/;
 int n;
 double dis(node a,node b)
 {
     return sqrt(((a.x-b.x)*(a.x-b.x))+((a.y-b.y)*(a.y-b.y)));
 }
 bool cmp(node a,node b)
 {
     if(a.x==b.x) return a.y<b.y;
     return a.x<b.x;
 }
 bool Cross(node a,node b,node c)
 {
     double x1=a.x-b.x,y1=a.y-b.y;
     double x2=c.x-b.x,y2=c.y-b.y;
     if((x1*y2-x2*y1)<=) return ;
     //如果不希望在凸包的边上有输入点。把<=改成<
     return ;
 }
 int Andrew()
 {
     sort(p+,p+n+,cmp);
     int num=;
     for(int i=;i<=n;i++)
     {
         while(num>&&!Cross(s[num-],s[num-],p[i]))
             num--;
         s[num++]=p[i];
     }
     int tmp=num;
     for(int i=n-;i>=;i--)
     {
         while(num>tmp&&!Cross(s[num-],s[num-],p[i]))
             num--;
         s[num++]=p[i];
     }
     if(n>) num--;
     return num;
 }
 int main()
 {
     //freopen("shuttle.in","r",stdin);
     //freopen("shuttle.out","w",stdout);
     scanf("%d",&n);
     for(int i=;i<=n;i++)
         scanf("%lf %lf",&p[i].x,&p[i].y);
     int num=Andrew();
     double sum=;
     for(int i=;i<=num-;i++)
         sum+=dis(s[i],s[i+]);
     sum+=dis(s[num],s[]);//还有第n个点到第1个点的距离
     printf("%.2lf",sum);
     return ;
 }

Code