BP原理 - 前向计算与反向传播实例

Outline

前向计算

反向传播

很多事情不是需要聪明一点，而是需要耐心一点，踏下心来认真看真的很简单的。

假设有这样一个网络层：

第一层是输入层，包含两个神经元i1 i2和截距b1；

第二层是隐含层，包含两个神经元h1 h2和截距b2，

第三层是输出o1,o2，每条线上标的wi是层与层之间连接的权重，激活函数默认为sigmoid函数。

赋初值为：

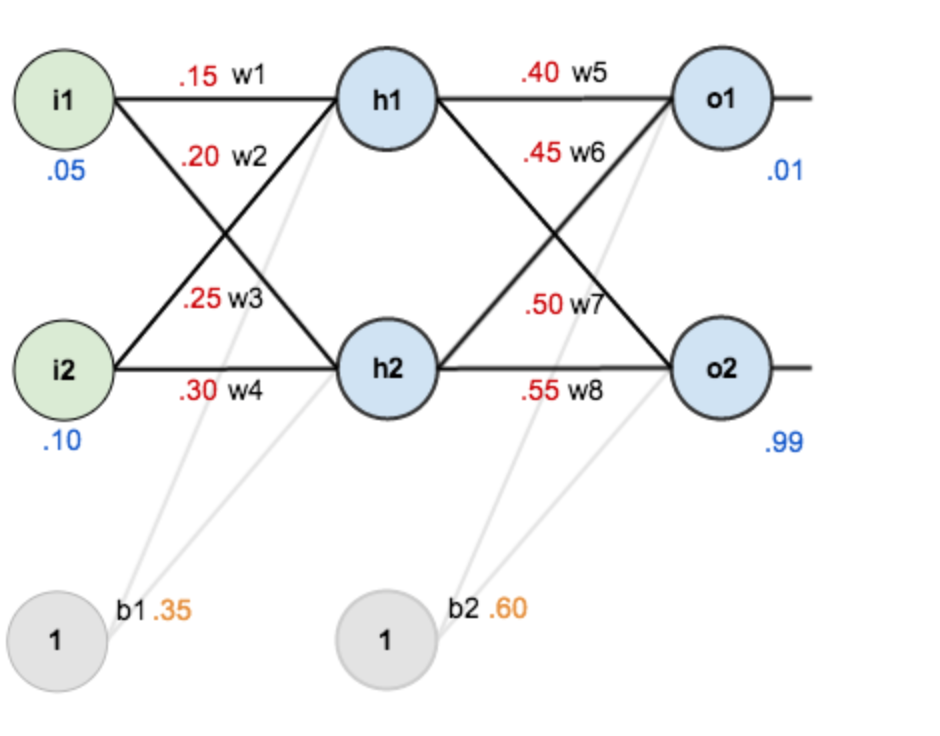
输入数据  i1=0.05，i2=0.10;

输出数据  o1=0.01, o2=0.99;

初始权重  w1=0.15,w2=0.20,w3=0.25,w4=0.30;

　　　　  w5=0.40,w6=0.45,w7=0.50,w8=0.55

目标：给出输入数据i1,i2(0.05和0.10)，使输出尽可能与原始输出o1,o2(0.01和0.99)接近。

Step 1 前向计算

1. 输入层—>隐含层：

计算神经元h1的输入加权和：

神经元h1的输出o1:(此处用到激活函数为sigmoid函数)：

同理，可计算出神经元h2的输出o2：

2. 隐含层—>输出层：

计算输出层神经元o1的值：

同理，计算o2：

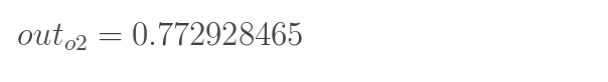
前向计算过程结束，得到输出值为[0.75136079 , 0.772928465]，与实际值[0.01 , 0.99]相差很远，对误差进行反向传播，更新权值，重新计算输出。

Step 2 反向传播

1. 计算总误差

总误差：(square error)

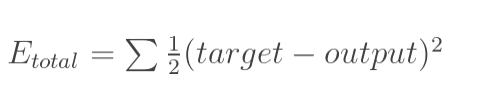
分别计算o1和o2的误差，总误差为两者之和：

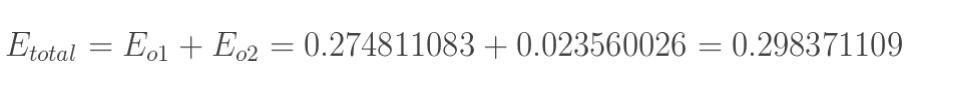
2. 输出层—>隐含层的权值更新

以权重参数w5为例，如果想知道w5对整体误差产生了多少影响，用整体误差对w5求偏导求出：（链式法则）

如图所示：

现在分别计算每个式子的值：  loss--Sigmoid--weight

计算：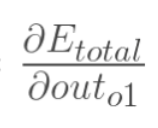

计算下一步之前，先来看一下Sigmoid函数求导：

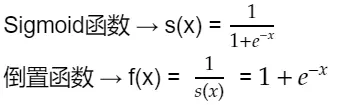
根据倒数法则从f(x)开始推导得出：

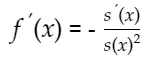
有以上两个式子可推出：

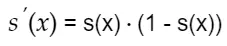
计算：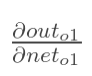

计算：

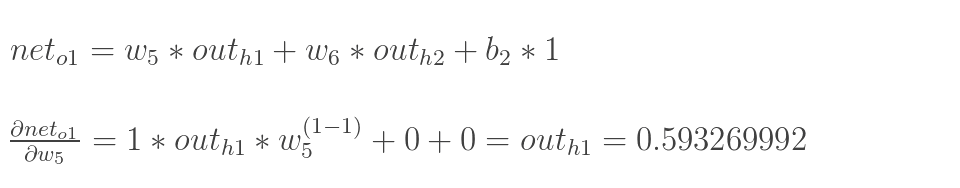
最后三者相乘：

这样我们就计算出整体误差E(total)对w5的偏导值。

综合以上四步计算过程可得：

为了表达方便，用来表示输出层的误差：

因此，整体误差E(total)对w5的偏导公式可以写成：

如果输出层误差计为负的话，也可以写成：

最后，更新w5的值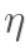，是学习速率，这里设为0.5：

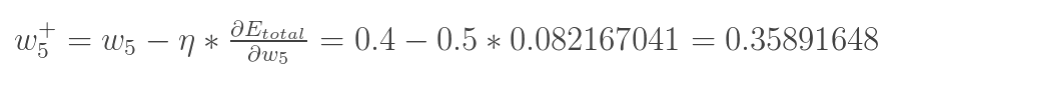
同理，可更新w6,w7,w8:

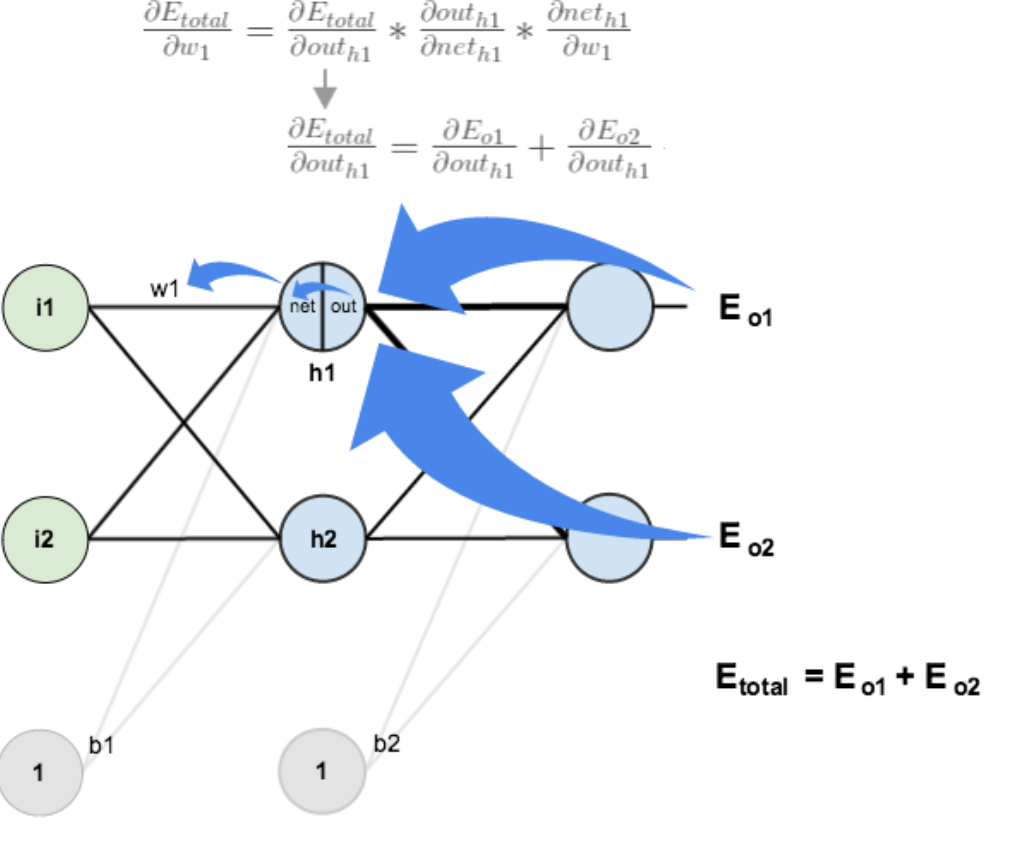
3. 隐含层—>输入层的权值更新

上一部分传播过程为：out(o1)—>net(o1)—>w5；

此处：out(h1)—>net(h1)—>w1，注意out(h1)会接受E(o1)和E(o2)两个地方传来的误差，两个都要计算。

计算：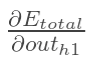

先计算：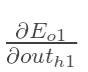

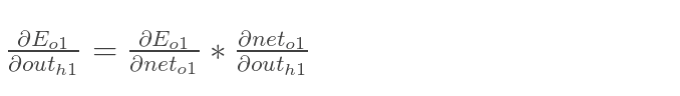
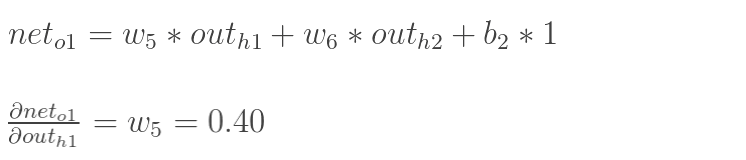
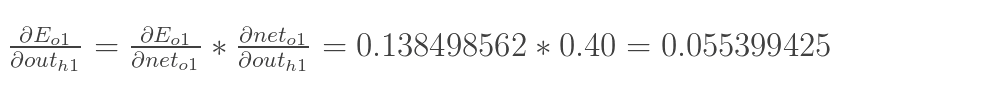
同理，计算出：

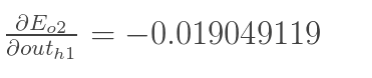
两者相加得到总值：

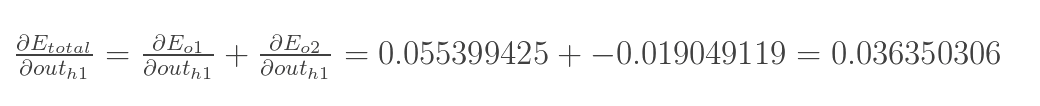
再计算：

再计算：

最后，三者相乘：

为了简化公式，用sigma(h1)表示隐含层单元h1的误差：

最后，更新w1的权值：

同理，额可更新w2,w3,w4的权值：

一次误差的反向传播完成，之后再把更新的权值重新计算，得到新的误差，该例中第一次迭代之后，总误差E(total)由0.298371109下降至0.291027924。迭代10000次后，总误差为0.000035085，输出为[0.015912196,0.984065734](原输入为[0.01,0.99])。