HDU-5728-PowMod-求phi(i*n)前缀和+指数循环节

HDU-5728-PowMod-求phi(i*n)前缀和+指数循环节

---

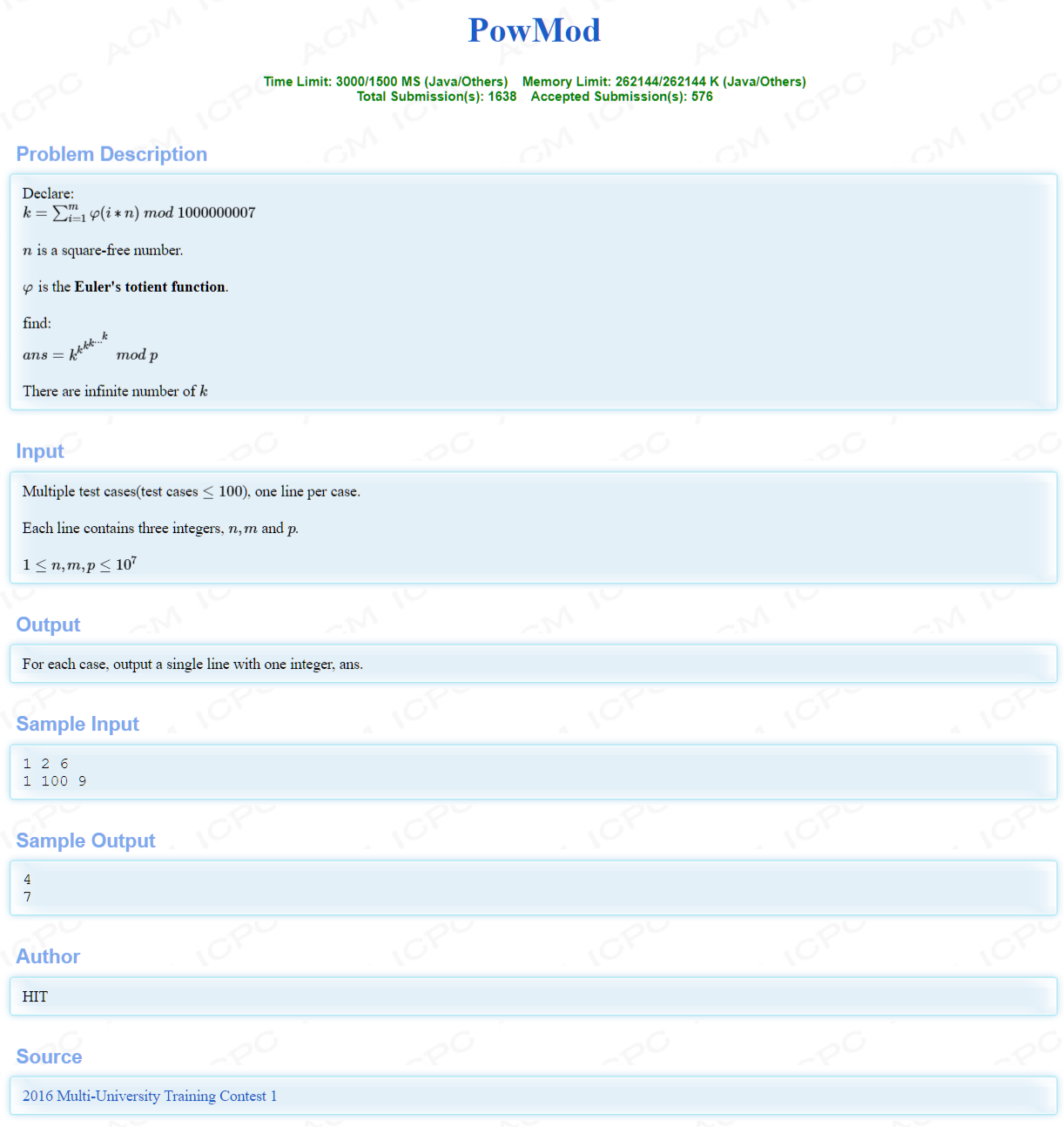
【Problem Description】

令\(k=\sum_{i=1}^m \varphi(i\cdot n)\ mod \ (10^9+7)\)。求\(k^{k^{k^{\dots}}}\ mod \ p\)。

【Solution】

因为\(n\)的所有质因子的幂次都为\(1\)，所以有\(gcd(p,\frac{n}{p})=1\)。其中\(p\)为\(n\)的最小质因子

• 假设\(i\ mod \ p\ne 0\)，则有\(gcd(i\cdot \frac{n}{p},p)=1\)。因此有\(\varphi(i\cdot n)=\varphi(i\cdot \frac{n}{p}\cdot p)=\varphi(i\cdot \frac{n}{p})\cdot \varphi(p)\)。
• 假设\(i\ mod \ p=0\)，则有\(gcd(i\cdot \frac{n}{p},p)=p\)。因此有\(\varphi(i\cdot n)=\varphi(i\cdot \frac{n}{p}\cdot p)=\varphi(i\cdot \frac{n}{p})\cdot p\)。

根据以上两条性质可得，令\(f(m,n)=\sum_{i=1}^m\varphi(i\cdot n)\)：

\[f(m,n)=\sum_{i\ mod\ p\ne 0}\varphi(i\cdot \frac{n}{p})\cdot \varphi(p)+\sum_{i\ mod\ p=0}\varphi(i\cdot \frac{n}{p})\cdot p
\\=\varphi(p)\sum_{i\ mod\ p\ne 0}\varphi(i\cdot \frac{n}{p})+\sum_{i\ mod \ p=0}\varphi(i\cdot \frac{n}{p})\cdot(\varphi(p)+1)
\\=\varphi(p)\cdot\Bigg(\sum_{i\ mod\ p\ne0}\varphi(i\cdot \frac{n}{p})+\sum_{i\ mod\ p=0}\varphi(i\cdot \frac{n}{p}) \Bigg)+\sum_{i\ mod \ p=0}\varphi(i\cdot \frac{n}{p})
\\=\varphi(p)\cdot\sum_{i=1}^m\varphi(i\cdot \frac{n}{p})+\sum_{i=1}^{\frac{m}{p}}\varphi(i\cdot n)
\]

所以可得：\(f(m,n)=\varphi(p)\cdot f(m,\frac{n}{p})+f(\frac{n}{p},n)\)。这是一个递推式，可用递归求得。到此我们求得了\(k\)的值。

对于\(k^{k^{k^{\dots}}}\ mod \ p\)可以用扩展欧拉定理进行欧拉降幂即可。

---

【Code】

/*
 * @Author: Simon
 * @Date: 2019-09-02 18:00:24
 * @Last Modified by: Simon
 * @Last Modified time: 2019-09-02 20:22:51
 */
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define maxn 10000005
typedef long long LL;
const int mod=1e9+7;
int prime[maxn],cnt=0;
LL phi[maxn],sum[maxn];
bool vis[maxn];
void Euler(){
    phi[1]=1;
    for(int i=2;i<maxn;i++){
        if(!vis[i]){
            prime[++cnt]=i;
            phi[i]=i-1;
        }
        for(int j=1;j<=cnt&&i*prime[j]<maxn;j++){
            vis[i*prime[j]]=1;
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            phi[i*prime[j]]=phi[i]*(prime[j]-1);
        }
    }
    for(int i=1;i<maxn;i++) sum[i]=(sum[i-1]+phi[i])%mod;
}
int dfs(int m,int n){
    if(n==1) return sum[m];
    if(m==0) return 0;
    for(int i=2;i*i<=n;i++){ //找最小质因子
        if(n%i==0){
            return (phi[i]*1LL*dfs(m,n/i)%mod+dfs(m/i,n))%mod;
        }
    }
    if(n>1) return (phi[n]*dfs(m,n/n)%mod+dfs(m/n,n))%mod; //n本身就是素数
}
int gcd(int a,int b){
    return b==0?a:gcd(b,a%b);
}
int fpow(int a,int b,int mod){
    a%=mod;int ans=1;
    while(b){
        if(b&1) ans=ans*1LL*a%mod;
        a=a*1LL*a%mod;
        b>>=1;
    }
    return ans;
}
int f(int k,int m){ //递归欧拉降幂
    if(m==1) return 0;
    int p=phi[m];
    int t=f(k,p);
    int g=gcd(k,m);
    if(g==1) return fpow(k,t,m);
    else return fpow(k,t+p,m);
}
int main(){
#ifndef ONLINE_JUDGE
    //freopen("input.in","r",stdin);
    //freopen("output.out","w",stdout);
#endif
    ios::sync_with_stdio(false);
    cin.tie(0);Euler();
    int n,m,p;
    while(cin>>n>>m>>p){
        int k=dfs(m,n);
        cout<<f(k,p)%p<<endl;
    }
#ifndef ONLINE_JUDGE
    cout<<endl;system("pause");
#endif
    return 0;
}