[Comet OJ - Contest #6 D][48D 2280]另一道树题_并查集

另一道树题

题目大意：

数据范围：

---

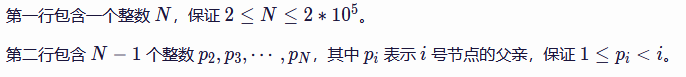
题解：

这个题第一眼能发现的是，我们的答案分成两种情况。

第一种是在非根节点汇合，第二种是在根节点汇合。

尝试枚举在第几回合结束，假设在第$i$回合结束的方案数为$f_i$，那么总答案就是$\sum\limits_{i = 1} ^ {N - 1}i\times f_i$。

显然没法求这个$f_i$....

进而，觉得这鬼东西的后缀和好像比较好求，就是$g _ i = \sum\limits_{j = i} ^ {N - 1} f _ j$。

由于我们就相当于对于深度相等的点的讨论，不难想到$bfs$序。

只考虑不在根节点汇合的情况。

发现，其实就是一段连续的区间，他们在$i$不小于一个值的时候，最多只能选取一个值。

也就是说随着我们枚举的回合数递增，这些连续的区间会存在一些合并的情况。

至于什么时候合并呢？其实就根据，相邻两个点到其$lca$的深度有关（这两个点的深度得相等），就是在这个深度差恰好等于回合数的时候，我们实施合并操作。

这样就完美的解决了不是非根汇合的情况。

考虑在根节点汇合咋办。

其实就相当于，随着回合数递增，所有深度不大于$i$的点只能选一个，就相当于和根节点合并咯。

总之通通用并查集维护就好了。

代码：

#include <bits/stdc++.h>

#define N 200010 

using namespace std;

int head[N], to[N << 1], nxt[N << 1], tot;

struct Node {
	int x, y;
};

vector <Node> v[N];

queue <int> q;

int f[20][N], g[N], F[N], S[N], dep[N], dic[N], n, inv[N];

const int mod = 998244353 ;

typedef long long ll;

char *p1, *p2, buf[100000];

#define nc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1 ++ )

int rd() {
	int x = 0, f = 1;
	char c = nc();
	while (c < 48) {
		if (c == '-')
			f = -1;
		c = nc();
	}
	while (c > 47) {
		x = (((x << 2) + x) << 1) + (c ^ 48), c = nc();
	}
	return x * f;
}

int qpow(int x, int y) {
	int ans = 1;
	while (y) {
		if (y & 1) {
			ans = (ll)ans * x % mod;
		}
		y >>= 1;
		x = (ll)x * x % mod;
	}
	return ans;
}

inline void add(int x, int y) {
	to[ ++ tot] = y;
	nxt[tot] = head[x];
	head[x] = tot;
}

int lca(int x, int y) {
	if (dep[x] < dep[y])
		swap(x, y);
	for (int i = 19; ~i; i -- ) {
		if (dep[f[i][x]] >= dep[y]) {
			x = f[i][x];
		}
	}
	if (x == y)
		return x;
	for (int i = 19; ~i; i -- ) {
		if (f[i][x] != f[i][y]) {
			x = f[i][x];
			y = f[i][y];
		}
	}
	return f[0][x];
}

void dfs(int p, int fa) {
	v[dep[p]].push_back((Node){1, p});
	f[0][p] = fa;
	for (int i = 1; i <= 19; i ++ ) {
		f[i][p] = f[i - 1][f[i - 1][p]];
	}
	for (int i = head[p]; i; i = nxt[i]) {
		if (to[i] != fa) {
			dep[to[i]] = dep[p] + 1;
			dfs(to[i], p);
		}
	}
}

void bfs() {
	while (!q.empty())
		q.pop();
	q.push(1);
	int cnt = 0;
	while (!q.empty()) {
		int x = q.front();
		q.pop();
		dic[ ++ cnt] = x;
		for (int i = head[x]; i; i = nxt[i]) {
			if (to[i] != f[0][x]) {
				q.push(to[i]);
			}
		}
	}
	for (int i = 1; i < n; i ++ ) {
		if (dep[dic[i]] == dep[dic[i + 1]]) {
			v[dep[dic[i]] - dep[lca(dic[i], dic[i + 1])]].push_back((Node) {dic[i], dic[i + 1]});
		}
	}
}

int find(int x) {
	return F[x] == x ? x : F[x] = find(F[x]);
}

int main() {
	n = rd();
	for (int i = 1; i <= n; i ++ ) {
		F[i] = i;
		S[i] = 1;
	}
	for (int i = 2; i <= n; i ++ ) {
		int x = rd();
		add(x, i);
		add(i, x);
	}
	dfs(1, 1);
	bfs();
	inv[0] = 1;
	for (int i = 1; i <= n; i ++ )
		inv[i] = qpow(i, mod - 2);

	// for (int i = 0 ; i <= n; i ++ ) {
	// 	printf("%d ", inv[i]);
	// }
	// puts("");

	int mdl = qpow(2, n);
	for (int i = 1; i < n; i ++ ) {
		g[i] = (mdl - n - 1 + mod) % mod;
		int len = v[i].size();
		for (int j = 0; j < len; j ++ ) {
			int x = v[i][j].x, y = v[i][j].y;
			x = find(x), y = find(y);
			if (x != y) {
				mdl = (ll)mdl * inv[S[x] + 1] % mod * inv[S[y] + 1] % mod;
				F[x] = y; S[y] += S[x];
				mdl = (ll)mdl * (S[y] + 1) % mod;
			}
		}
	}
	int ans = 0;
	for (int i = 1; i < n; i ++ ) {
		ans = (ans + (ll)(g[i] - g[i + 1] + mod) % mod * i % mod) % mod;
	}
	cout << ans << endl ;
	return 0;
}

小结：好题好题，这个题的思路行云流水。重点是能否想到把那个，一段区间只能选一个这个事情考虑清楚，从而转变成区间的合并问题，这是关键。