leetcode-63. Unique Paths II · DP + vector

题面

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

Now consider if some obstacles are added to the grids. How many unique paths would there be?

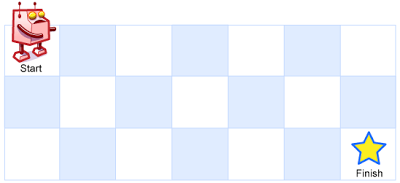
类似我们做过的62. Unique Paths，给定矩阵，其中0-无障碍物， 1-有障碍物（无法通过），找出到达右下角的不重复的路径数。

样例

1. Input:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
Output: 2
Explanation:
There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

2. Input

[[0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1],[0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0],[1,1,1,0,0,0,0,1,0,0,0,0,0,0,0,0,1,0,0,1,1,0,0,0,0,0,0,0,0,1,0,0,1],[0,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0],[0,0,0,1,0,1,0,0,0,0,1,1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,1,1,0],[1,0,1,1,1,0,0,0,0,1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,0],[0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,1,0,0,0,1,0,1,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,1,0],[0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,1,0,0,0,0,0],[0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0],[1,0,1,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,1,0,1,0,0,0,0,1],[0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,0,0,0,1,1,0,0,0,0,0],[0,1,0,1,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,0,0,0,0,0],[0,1,0,0,0,0,0,0,1,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,1,0,1],[1,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,1,0,0,1,0,0,0,0,0,0],[0,0,1,0,0,0,0,0,0,0,1,0,0,1,0,0,1,0,0,0,0,0,0,1,1,0,1,0,0,0,0,1,1],[0,1,0,0,1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,1,0,1,1,0,1,0,1],[1,1,1,0,1,0,0,0,0,1,0,0,0,0,0,0,1,0,1,0,1,1,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,0,0,1,1],[0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,1,0,0,0]]

这个样例是做的过程中，遇到的一个棘手样例。int 会爆

Output : 1637984640

思路

我们采用和62. Unique Paths一样的思路，到达某点的路径数就是到达它的上边点和左边点路径数的和，只不过要注意的是，当有障碍物时，该点的路径数就要置0（无法到达该点）

算法（直接采用空间压缩DP算法）

时间复杂度：O(m*n)

空间复杂度：O(n)

1. 新建dp[n]，预处理第一行（只能往右走，所以出现障碍物之后的点都无法到达置0， 之前的置1）

2. 遍历给定二位矩阵，第一列单独处理（没有左边的点），如果该点为1，即有障碍物，那么该点路径数置0；

3. 其他点正常处理，如果给定矩阵该点为1，即有障碍物，那么dp数组对应点置0；否则，该点路径加和左边点路径。

4. 返回dp末尾元素置。

源码

 class Solution {
 public:
     int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
         int row = obstacleGrid.size(), col = obstacleGrid[].size();
         vector<unsigned int> dp(col, );//采用unsigned int 应对样例2的数据
         for(int i=; i<col; i++)//第一行预处理
         {
             if(obstacleGrid[][i] == )
                 break;
             dp[i] = ;
         }
         for(int i=; i<row; i++)
         {
             if(obstacleGrid[i][] == )//第一列特殊处理
                 dp[] = ;
             for(int j=; j<col; j++)//处理其他元素
             {
                 if(obstacleGrid[i][j] == )//遇到障碍物，无法通过置0
                     dp[j] = ;
                 else
                     dp[j] += dp[j-];//可以通过，加和左边点路径。
             }
         }
         return dp[col-];
     }
 };

注意

这里用了一维DP数组来做，用二维DP也可以，结果差不多。

二维DP源码

和一维大同小异

时间复杂度：O(m*n)

空间复杂度：O(m*n)

 class Solution {
 public:
     int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
         int row = obstacleGrid.size(), col = obstacleGrid[].size();
         vector<vector<unsigned int>> dp(row, vector<unsigned int>(col, ));//二维vector你get了吗？
         for(int i=; i<col; i++)
         {
             if(obstacleGrid[][i] == )
                 break;
             dp[][i] = ;
         }
         for(int i=; i<row; i++)
         {
             if(obstacleGrid[i][] == )
                 break;
             dp[i][] = ;
         }
         for(int i=; i<row; i++)
         {
             for(int j=; j<col; j++)
             {
                 if(obstacleGrid[i][j] == )
                     dp[i][j] = ;
                 else
                     dp[i][j] = dp[i][j-] + dp[i-][j];
             }
         }
         return dp[row-][col-];
     }
 };