php实现数组中的逆序对(归并排序实现:排序 辅助数组)
php实现数组中的逆序对(归并排序实现:排序 辅助数组)
一、总结
这题用归并排序 线段树 树状数组 等操作的复杂度应该都是小于n方的
二、php实现数组中的逆序对
题目描述
输入描述:
题目保证输入的数组中没有的相同的数字
数据范围:
对于%50的数据,size<=10^4
对于%75的数据,size<=10^5
对于%100的数据,size<=2*10^5
输入
1,2,3,4,5,6,7,0
输出
7
三、代码
class Solution {
public:
int InversePairs(vector<int> data) {
int length=data.size();
if(length<=0)
return 0;
//vector<int> copy=new vector<int>[length];
vector<int> copy;
for(int i=0;i<length;i++)
copy.push_back(data[i]);
long long count=InversePairsCore(data,copy,0,length-1);
//delete[]copy;
return count%1000000007;
}
long long InversePairsCore(vector<int> &data,vector<int> ©,int start,int end)
{
if(start==end)
{
copy[start]=data[start];
return 0;
}
int length=(end-start)/2;
long long left=InversePairsCore(copy,data,start,start+length);
long long right=InversePairsCore(copy,data,start+length+1,end);
int i=start+length;
int j=end;
int indexcopy=end;
long long count=0;
while(i>=start&&j>=start+length+1)
{
if(data[i]>data[j])
{
copy[indexcopy--]=data[i--];
count=count+j-start-length; //count=count+j-(start+length+1)+1;
}
else
{
copy[indexcopy--]=data[j--];
}
}
for(;i>=start;i--)
copy[indexcopy--]=data[i];
for(;j>=start+length+1;j--)
copy[indexcopy--]=data[j];
return left+right+count;
}
};
php实现数组中的逆序对(归并排序实现:排序 辅助数组)的更多相关文章
- 力扣Leetcode 面试题51. 数组中的逆序对 - 归并排序
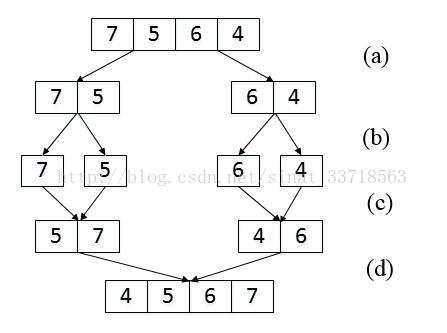
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对.输入一个数组,求出这个数组中的逆序对的总数. 示例 1: 输入: [7,5,6,4] 输出: 5 限制: 0 <= ...
- 剑指 Offer 51. 数组中的逆序对 + 归并排序 + 树状数组
剑指 Offer 51. 数组中的逆序对 Offer_51 题目描述 方法一:暴力法(双层循环,超时) package com.walegarrett.offer; /** * @Author Wal ...
- 九度OJ 1348 数组中的逆序对 -- 归并排序
题目地址:http://ac.jobdu.com/problem.php?pid=1348 题目描述: 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对.输入一个数组,求 ...
- 求数组中的逆序对的数量----剑指offer36题
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对.输入一个数组,求出这个数组中的逆序对的总数: 如数组{7,5,6,4},逆序对总共有5对,{7,5},{7,6},{7, ...
- 九度OJ 1348:数组中的逆序对 (排序、归并排序)
时间限制:1 秒 内存限制:32 兆 特殊判题:否 提交:2777 解决:656 题目描述: 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对.输入一个数组,求出这个数组 ...
- 剑指Offer——数组中的逆序对(归并排序的应用)
蛮力: 遍历数组,对每个元素都往前遍历所有元素,如果有发现比它小的元素,就count++. 最后返回count取模. 结果没问题,但超时哈哈哈,只能过50%. 归并法: 看讨论,知道了这道题的经典 ...
- 归并排序(归并排序求逆序对数)--16--归并排序--Leetcode面试题51.数组中的逆序对
面试题51. 数组中的逆序对 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对.输入一个数组,求出这个数组中的逆序对的总数. 示例 1: 输入: [7,5,6,4] 输出 ...
- MergeSort归并排序和利用归并排序计算出数组中的逆序对
首先先上LeetCode今天的每日一题(面试题51. 数组中的逆序对): 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对.输入一个数组,求出这个数组中的逆序对的总数. ...
- [剑指OFFER] 数组中的逆序对
题目描述 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对.输入一个数组,求出这个数组中的逆序对的总数. 分析:利用归并排序的思想,分成2部分,每一部分按照从大到 ...
随机推荐
- vue ---webpack 打包上线
先来描述一下期间遇到的问题有哪些: 1.打包后将 dist 文件夹和 index.html 放到 tomcat,在浏览器中访问时,出现空白页,f12 提示 404. 2.打包好的静态资源均是绝对路径 ...
- 74.sscanf数据扫描
"%[0-9A-Za-z] 读取一个集合,遇到不是数组或者大小写字母跳出 %*[^0-9A-Za-z]读取所有的非数字字母的字符,忽略 示例: ]= "123sadsadasd ...
- Fedora 13 Alpha测试手记横空出世
本文转载在:http://www.linux521.com/2009/system/201004/10719.html 本文是继<Fedora 11-Alpha试用手记>文章(http ...
- BZOJ1444: [Jsoi2009]有趣的游戏(Trie图,矩乘)
Description Input 注意 是0<=P, n , l, m≤ 10. Output Sample Input input 1 3 2 2 1 2 1 2 AB BA AA inpu ...
- CISP/CISA 每日一题 八
CISA 每日一题(答)网关执行电子邮件格式转换 电子邮件安全——加密 大文件——对称加密 不可否认——非对称 哈希——完整性 电子银行主要风险: 战略.经营和声誉上的风险 双SSP每日一题 ...
- 【2017 Multi-University Training Contest - Team 9】FFF at Valentine
[链接]http://acm.hdu.edu.cn/showproblem.php?pid=6165 [题意] 一张有向图,n个点,m条边,保证没有重边和自环.询问任意两个点能否满足任何一方能够到达另 ...
- 设计模式六大原则(二):里氏替换原则(Liskov Substitution Principle)
里氏替换原则(LSP)由来: 最早是在 妖久八八 年, 由麻神理工学院得一个女士所提出来的. 定义: 1:如果对每一个类型为 T1的对象 o1,都有类型为 T2 的对象o2,使得以 T1定义的所有程序 ...
- virtualtemplate 接口
虚拟接口的配置.建立.与实际接口的关联 VPN在会话连接建立之后.须要创建一个虚拟接口用于和对端之间数据传输.此时,将依照用户配置,选择一个虚拟接口模板,动态地创建一个虚拟接口. 该接口将在会话结束时 ...
- Android LruCache类分析
public class LurCache<K, V> { private final LinkedHashMap<K, V> map; private int size; / ...
- nuxt.js配置BASE_URL(基本域名)和NODE_ENV(环境变量)
一直以来,开发环境和生产环境的数据接口域名不一样总是困扰着我 每次打测试包或者线上包,我都得手动切换域名,我相信很多人的做法跟这差不多,类似下面这样: (你已经注意到,这个文件已经被我无情的删除了,因 ...
