poj 3498 March of the Penguins（拆点+枚举汇点 最大流）

March of the Penguins

Time Limit: 8000MS		Memory Limit: 65536K
Total Submissions: 4873		Accepted: 2220

Description

Somewhere near the south pole, a number of penguins are standing on a number of ice floes. Being social animals, the penguins would like to get together, all on the same floe. The penguins do not want to get wet, so they have use their limited jump distance to get together by jumping from piece to piece. However, temperatures have been high lately, and the floes are showing cracks, and they get damaged further by the force needed to jump to another floe. Fortunately the penguins are real experts on cracking ice floes, and know exactly how many times a penguin can jump off each floe before it disintegrates and disappears. Landing on an ice floe does not damage it. You have to help the penguins find all floes where they can meet.

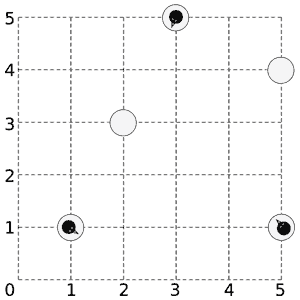
A sample layout of ice floes with 3 penguins on them.

Input

On the first line one positive number: the number of testcases, at most 100. After that per testcase:

• One line with the integer N (1 ≤ N ≤ 100) and a floating-point number D (0 ≤ D ≤ 100 000), denoting the number of ice pieces and the maximum distance a penguin can jump.

• N lines, each line containing x_i, y_i, n_i and m_i, denoting for each ice piece its X and Y coordinate, the number of penguins on it and the maximum number of times a penguin can jump off this piece before it disappears (−10 000 ≤ x_i, y_i ≤ 10 000, 0 ≤ n_i ≤ 10, 1 ≤ m_i ≤ 200).

Output

Per testcase:

• One line containing a space-separated list of 0-based indices of the pieces on which all penguins can meet. If no such piece exists, output a line with the single number −1.

Sample Input

2
5 3.5
1 1 1 1
2 3 0 1
3 5 1 1
5 1 1 1
5 4 0 1
3 1.1
-1 0 5 10
0 0 3 9
2 0 1 1

Sample Output

1 2 4
-1

Source

Northwestern Europe 2007

题意：给你n个冰岛 有些岛上有企鹅  给定岛的坐标  已经岛上面的企鹅数  和当多少只企鹅离开岛会下沉

D表示企鹅能跳跃的距离

现在所有的企鹅要汇聚到一个岛上去 问你那些岛可以符合

题解：就是将一个岛进行拆点  拆成两个点 之间的容量就是最大运行多少企鹅走的数量

构图  求最大流是不是等于所有的企鹅数

因为100个点  所有我们可以选择枚举每个点 看看是否满足

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cstdlib>
 #include<string.h>
 #include<set>
 #include<vector>
 #include<queue>
 #include<stack>
 #include<map>
 #include<cmath>
 typedef long long ll;
 typedef unsigned long long LL;
 using namespace std;
 const double PI=acos(-1.0);
 const double eps=0.0000000001;
 const int INF=1e9;
 const int N=+;
 int b[N];
 int head[N];
 int tot;
 struct node{
     int to,next,flow;
 }edge[N<<];
 struct Node{
     double x,y;
     int m,k;
 }a[N];
 void init(){
     memset(head,-,sizeof(head));
     tot=;
 }
 void add(int u,int v,int flow){
     edge[tot].to=v;
     edge[tot].flow=flow;
     edge[tot].next=head[u];
     head[u]=tot++;

     edge[tot].to=u;
     edge[tot].flow=;
     edge[tot].next=head[v];
     head[v]=tot++;
 }
 int dis[N];
 int BFS(int s,int t){
     queue<int>q;
     memset(dis,-,sizeof(dis));
     q.push(s);
     dis[s]=;
     while(!q.empty()){
         int x=q.front();
         q.pop();
         if(x==t)return ;
         for(int i=head[x];i!=-;i=edge[i].next){
             int v=edge[i].to;
             if(dis[v]==-&&edge[i].flow){
                 dis[v]=dis[x]+;
                 q.push(v);
             }
         }
     }
     if(dis[t]==-)return ;
     return ;
 }
 int DFS(int s,int flow,int t){
     if(s==t)return flow;
     int ans=;
     for(int i=head[s];i!=-;i=edge[i].next){
         //cout<<34<<endl;
         int v=edge[i].to;
         if(edge[i].flow&&dis[v]==dis[s]+){
             int f=DFS(v,min(flow-ans,edge[i].flow),t);
             edge[i].flow-=f;
             edge[i^].flow+=f;
             ans+=f;
             if(ans==flow)return ans;
         }
     }
     return ans;
 }
 int Dinc(int s,int t){
     int flow=;
     while(BFS(s,t)){
        // cout<<4<<endl;
         flow=flow+DFS(s,INF,t);
     }
     return flow;
 }
 int main(){
     int tt;
     scanf("%d",&tt);
     while(tt--){
         int n;
         double d;
         int s,t;
         scanf("%d%lf",&n,&d);
         int sum=;
         for(int i=;i<n;i++){
             scanf("%lf%lf%d%d",&a[i].x,&a[i].y,&a[i].m,&a[i].k);
             sum=sum+a[i].m;
         }
         s=*n+;
         t=*n+;
         int ss=;
         for(int kk=;kk<n;kk++){
             init();
             add(kk,t,INF);
             for(int i=;i<n;i++){
                 add(i,i+n,a[i].k);
                 add(s,i,a[i].m);
                 for(int j=i+;j<n;j++){
                     double dd=sqrt((a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y));
                     if(dd<=d){
                         add(i+n,j,INF);
                         add(j+n,i,INF);
                     }
                 }
             }
             if(Dinc(s,t)==sum){
                // cout<<kk<<endl;
                 b[ss++]=kk;
             }
         }
         if(ss==)cout<<-<<endl;
         else{
             cout<<b[];
             for(int i=;i<ss;i++)cout<<" "<<b[i];
             cout<<endl;
         }
     }
 }