MPI对道路车辆情况的Nagel-Schreckenberg 模型进行蒙特卡洛模拟

平台Ubuntu 16.04，Linux下MPI环境的安装见链接：https://blog.csdn.net/lusongno1/article/details/61709460

据 Nagel-Schreckenberg 模型，车辆的运动满足以下规则：

1.   假设当前速度是 v ，和前一辆车的距离为d。

2.   如果 d > v，它在下一秒的速度会提高到 v + 1 ，直到达到规定的最高限速。

3.   如果 d <= v，那么它在下一秒的速度会降低到 d - 1 。

4.   前三条完成后，司机还会以概率 p 随机减速1个单位，速度不会为负值。

5.   基于以上几点，车辆向前移动v（这里的v已经被更新）个单位。

实验规模：

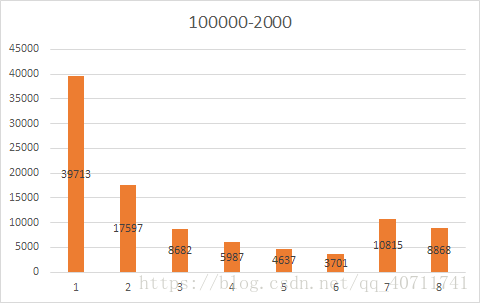
1. 车辆数量为100 000，模拟2000个周期后的道路情况。
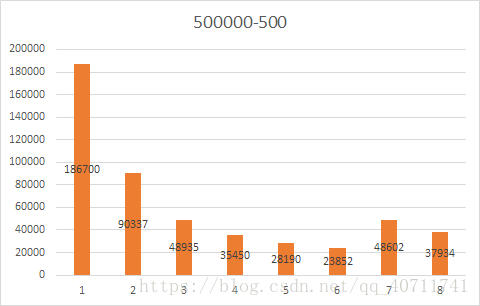
2. 车辆数量为 500 000 模拟 500个周期后的道路情况。
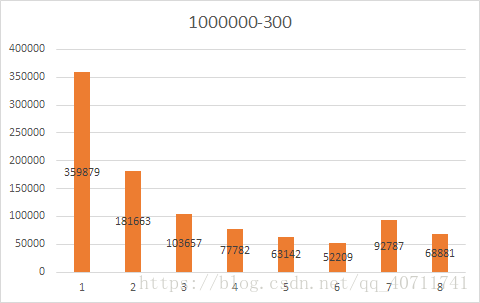
3. 车辆数量为 1 000 000 ，模拟300个周期后的道路情况。

实验设计：

初始化条件：

所有车辆初速度为4，车辆间距为8，最大速度为8，最小速度为1，最后一辆车的位置是0。减速概率为0.3

车辆结构体：

typedef struct car{
       int v;
       int d;
       int p;
}car;

所有车辆为一个数组car_list

核心循环：

//更新距离
car_list[i].d=car_list[i+1].p-car_list[i].p;//依赖于前一辆车
//更新速度
if(car_list[i].d>car_list[i].v&& car_list[i].v<vmax)car_list[i].v++;//加速
if(car_list[i].d<=car_list[i].v)car_list[i].v=car_list[i].d-1;//减速
if(car_list[i].v>1 && rand()%10< p )car_list[i].v--;//随机减速
//更新位置
car_list[i].p+=car_list[i].v;

对这段程序进行周期次数的循环

并行设计：

在每个周期中，按照核心数（0…N-1）将车辆分为N个连续的区间，每个核心计算各自的部分。

i=(num_car/numprocs*myid);//指向这个集合的第一个元素

除第一个核心外其他的进程K都需要在更新自己的车辆部分之前发送第一辆车的位置到进程K-1，除最后一个进程外的其他进程K都要在计算自己部分的最后一辆车时接受进程K+1发送的位置数据以更新最后一辆车。

为避免标准通信方式导致后面的进程要等待前面的进程执行到最后开始接受的时候才执行完发送，采用缓存通信方式（MPI_Bsend）。

if(myid!=0){//如果不是第一个线程就要向前发送数据
	MPI_Bsend(&(car_list[i].p),1,MPI_INT,myid-1,myid,MPI_COMM_WORLD);
}
//核心循环

if(myid!=numprocs-1){//不是最后一个进程
	MPI_Recv(&(temp),1,MPI_INT,myid+1,myid+1,MPI_COMM_WORLD,&status);
	//更新距离
	car_list[i].d=temp-car_list[i].p;
}

在周期结束之前要同步所有进程。

MPI_Barrier(MPI_COMM_WORLD);

输出结果：

只在四线程执行时输出到文件，将每个进程自己部分的车辆数据发送到第一个进程，第一个进程接收其它进程的数据整合后输出，并进行统计。

车辆的信息输出到result.txt中，格式为 进行输出的线程号 第几辆车：速度 位置 和前一辆车的距离

统计输出到statistic.txt中，前面输出的是速度统计，对应的速度有几辆车 。后面是位置统计，在位置范围有几辆车

结果分析：

可见不管哪种规模都会有大量的车处于速度为1的状态，随机减速会导致堵车情况。

运行时间分析：

10000

rank=0time:12.911823

rank=1time:12.937384

rank=2time:12.968312

rank=3time:12.837026

100000

rank=0time:127.054991

rank=1time:127.597898

rank=2time:127.428670

rank=3time:127.302298

rank=0time:169.043639

rank=1time:169.092520

rank=2time:169.038982

rank=0time:137.758731

rank=1time:137.782351

rank=0time:255.181992

500000

rank=0 time:158.620365

rank=1time:159.041463

rank=2time:158.827125

rank=3time:158.519957

rank=0time:211.242267

rank=1time:211.114535

rank=2time:211.117872

rank=0time:171.935731

rank=1time:171.970319

rank=0time:319.567614

1000000

rank=0 time:190.271859

rank=1time:190.056185

rank=2time:189.846401

rank=3time:190.314395

rank=0time:211.273677

rank=1time:211.328568

rank=2time:211.304030

rank=0time:172.247044

rank=1time:172.281147

rank=0time:318.965036

规模	时间/s
100k*2k	255	137	169	127
500k*0.5k	319	171	211	158
1000K*0.3k	318	172	211	190
加速比
100k*2k	1	1.861314	1.508876	2.007874
500k*0.5k	1	1.865497	1.511848	2.018987
1000K*0.3k	1	1.848837	1.507109	1.673684

实验遇到的问题：

1.如何串行执行

MPI的并行是进程的并行，所以MPI_Finalize()只是将资源释放了，并不是之后的程序就串行执行了，要想串行，可以指定一个进程执行。

2.结果输出

在用进程0输出所有车辆数据时发现只有线程0处理的部分数据有变更，其余数据维持在初始化时的状态。那么应该是每个进程是将处理了自己部分的数据的备份，而不是在原有数据的基础上处理的。所以要一个进程进行输出。

如果每个进程都自己输出数据就会产生文件写冲突而导致结果的不可预知，所以要将其它进程的数据发送到一个进程，用一个进程进行输出。

3.进程同步

如果进程间通信时设置的tag可以区分所有周期（比如设置为j*10+myid），那么在每个周期结束时就没有必要同步所有进程。

但是在这样修改之后运行时间没有什么区别，应该是核心的处理能力类似，同步产生的开销并不明显。

源程序：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <mpi.h>

int num_car=100000;
int num_cycle[]={2000,500,300};

const int v0=4,vmax=8,p=5;

typedef struct car
{
	int v;
	int d;
	int p;
}car;
car car_list[1000000];

int count[10]={0,0,0,0,0, 0,0,0,0,0};
int pos_count[20*8+10000*8]={0};//count per 100

int main(int argc,char *argv[])
{
	//四线程写结果的时候打开文件
	FILE*fp = fopen("result_100000.txt","w");
	FILE*fp2 = fopen("statistic_100000.txt","w");
	//初始条件

	int i=0;
	for(i=0;i<num_car;i++)
	{
		car_list[i].v=v0;
		car_list[i].p=vmax*i;
		car_list[i].d=vmax;
	}

    int     myid, numprocs;
    clock_t starttime,endtime;
    int    namelen;
    char   processor_name[MPI_MAX_PROCESSOR_NAME];

    MPI_Init(&argc,&argv);
    MPI_Comm_size(MPI_COMM_WORLD,&numprocs);
    MPI_Comm_rank(MPI_COMM_WORLD,&myid);

	int* mpi_buffer=malloc(sizeof(int)*1000000);
	MPI_Buffer_attach(mpi_buffer,sizeof(int)*1000000);

	//模拟过程开始
	starttime=clock();
	int j=0;
	for(j=0;j<2000;j++)
	{
		i=(num_car/numprocs*myid);//指向这个集合的第一个元素
		if(myid!=0)//如果不是第一个线程就要向前发送数据
		{
			MPI_Bsend(&(car_list[i].p),1,MPI_INT,myid-1,j*10+myid,MPI_COMM_WORLD);
		}

		for(;i<num_car/numprocs*(myid+1)-1;i++)
		{

			//更新距离
			car_list[i].d=car_list[i+1].p-car_list[i].p;
			//更新速度
			if(car_list[i].d>car_list[i].v && car_list[i].v<vmax)car_list[i].v++;
			if(car_list[i].d<=car_list[i].v)car_list[i].v=car_list[i].d-1;
			srand(i*num_car+j);
            if( car_list[i].v>1 )
            {
                int r=rand()%10;
                if(r<p)
                {
                    car_list[i].v--;
                    //printf("#");
                }
            }
			//更新位置
			car_list[i].p+=car_list[i].v;

		}
		if(myid!=numprocs-1)//不是最后一个进程
		{
			int temp;
			MPI_Status status;
			MPI_Recv(&(temp),1,MPI_INT,myid+1,j*10+myid+1,MPI_COMM_WORLD,&status);
			//更新距离
			car_list[i].d=temp-car_list[i].p;
			//printf("%d temp %d %d\n",myid,temp,car_list[i].d);
		}
        //更新速度
        if(car_list[i].v<vmax)car_list[i].v++;
		if(car_list[i].d<=car_list[i].v)car_list[i].v=car_list[i].d-1;
        srand((unsigned) time(NULL));
        if( car_list[i].v>1 && rand()%10< p )
        {
            car_list[i].v--;
        }
        //更新位置
        car_list[i].p+=car_list[i].v;

		//MPI_Barrier(MPI_COMM_WORLD);
    }//for cycle
    //模拟过程结束

    endtime=clock();
    printf("rank=%d time:%lf\n",myid,(double)(endtime-starttime)/CLOCKS_PER_SEC);
	//四线程的时候向文件写结果，别的线程时注释掉好了
	MPI_Barrier(MPI_COMM_WORLD);

	if(myid==0)
	{
		MPI_Send((car_list),sizeof(car)*num_car/4,MPI_BYTE,3,myid,MPI_COMM_WORLD);
	}
	if(myid==1)
	{
		MPI_Send((car_list+num_car/4),sizeof(car)*num_car/4,MPI_BYTE,3,myid,MPI_COMM_WORLD);
	}
	if(myid==2)
	{
		MPI_Send((car_list+2*num_car/4),sizeof(car)*num_car/4,MPI_BYTE,3,myid,MPI_COMM_WORLD);
	}
	if(myid==numprocs-1)
	{
		MPI_Status status;
		MPI_Recv((car_list),sizeof(car)*num_car/4,MPI_BYTE,0,0,MPI_COMM_WORLD,&status);
		MPI_Recv((car_list+num_car/4),sizeof(car)*num_car/4,MPI_BYTE,1,1,MPI_COMM_WORLD,&status);
		MPI_Recv((car_list+2*num_car/4),sizeof(car)*num_car/4,MPI_BYTE,2,2,MPI_COMM_WORLD,&status);		

		int a;
		for(a=0;a<num_car;a++)
		{
			fprintf(fp,"%d %d:%d %d %d\n",myid,a,car_list[a].v,car_list[a].p,car_list[a].d);
		}

		for(i=0;i<num_car;i++)
		{
			count[car_list[i].v]++;
			pos_count[car_list[i].p/1000]++;
		}

		int k;
		for(k=0;k<10;k++)
		{
			fprintf(fp2,"%d\t:%d\n",k,count[k]);
		}
		for(k=0;k<2*8+num_car*8/1000;k++)
		{
		    fprintf(fp2,"%d\t%d\n",k,pos_count[k]);
		}
	}

	MPI_Barrier(MPI_COMM_WORLD);
	fclose(fp);
	fclose(fp2);
    MPI_Finalize();

    return 0;
}