php实现记忆化递归--以斐波那契数列为例(还是以边学边做为主,注重练习)
php实现记忆化递归--以斐波那契数列为例(还是以边学边做为主,注重练习)
一、总结
1、递归不优化的话,30层开外就有点吃力了
2、php因为定义变量的时候不用定义变量类型,所以数组里面的类型也是php自动选择,这就会有下面的情况:
当int不够的时候自动转化为float,float不够的时候自动转化为科学计数法
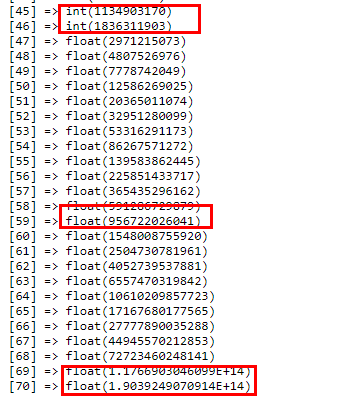
二、php实现记忆化递归--以斐波那契数列为例
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项。
三、代码
代码一
<?php $arr = array(0,1,1);
for($i=3;$i<=100;$i++){$arr[$i]=-1;}
function Fibonacci($n)
{
global $arr;
if($arr[$n]!=-1) return $arr[$n]; //1、边界情况都可以结合 记忆化递归数组判断,对比一下下面的代码就知道简便之处了
else{
$arr[$n-1]=$arr[$n-1]!=-1?$arr[$n-1]:Fibonacci($n-1);
$arr[$n-2]=$arr[$n-2]!=-1?$arr[$n-2]:Fibonacci($n-2);
return $arr[$n]=$arr[$n-1]+$arr[$n-2];
}
}
代码二
<?php
namespace app\index\controller; use app\index\controller\Base; class Exercise extends Base
{
public function index()
{
$this->FibonacciDemo();
} //斐波那契数列
private $arr = array();//记忆化递归数组
public function Fibonacci($n)
{
global $arr;
if($n==0) return 0;
else if($n==1||$n==2) return 1; //1、php中的逻辑连接符:和java一样,例如|表示位运算符,||表示逻辑运算符
else{
$arr[$n-1]=$arr[$n-1]!=-1?$arr[$n-1]:$this->Fibonacci($n-1);
$arr[$n-2]=$arr[$n-2]!=-1?$arr[$n-2]:$this->Fibonacci($n-2);
return $arr[$n]=$arr[$n-1]+$arr[$n-2]; //2、支持这样的返回方式,这应该是先赋值再返回 3、把求出的值给记录下数组,刚刚忘记记录$arr[$n]了
}
}
public function FibonacciDemo(){
global $arr;
for ($i=0; $i <100 ; $i++) {
$arr[$i]=-1;
}
$arr[0]=0;
$arr[1]=1;
$arr[2]=1;
echo($this->Fibonacci(50));
dump($arr);die;
} }
截图:
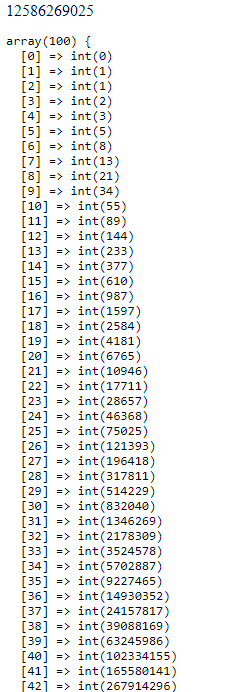
php实现记忆化递归--以斐波那契数列为例(还是以边学边做为主,注重练习)的更多相关文章
- 16位masm汇编实现记忆化递归搜索斐波那契数列第50项
.model small ;递归fib,使用压缩BCD码,小端派 .data y1 byte 6 dup(0) y2 byte 6 dup(0) vis byte 1,1,1,61 dup(0) ;便 ...
- Python递归及斐波那契数列
递归函数 在函数内部,可以调用其他函数.如果一个函数在内部调用自身本身,这个函数就是递归函数.举个例子,我们来计算阶乘 n! = 1 * 2 * 3 * ... * n,用函数 fact(n)表示,可 ...
- 【递归】斐波那契数列第n个数
递归.递推计算斐波那契数列第n项的值: #include <stdio.h> long long fact(int n); //[递推]计算波那契数列第n个数 long long fact ...
- Python编程笔记(第三篇)【补充】三元运算、文件处理、检测文件编码、递归、斐波那契数列、名称空间、作用域、生成器
一.三元运算 三元运算又称三目运算,是对简单的条件语句的简写,如: 简单条件处理: if 条件成立: val = 1 else: val = 2 改成三元运算 val = 1 if 条件成立 else ...
- python递归与非递归实现斐波那契数列
1.题目描述 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0). 递归实现: class Solution(): def Fibnacci(self ...
- 以计算斐波那契数列为例说说动态规划算法(Dynamic Programming Algorithm Overlapping subproblems Optimal substructure Memoization Tabulation)
动态规划(Dynamic Programming)是求解决策过程(decision process)最优化的数学方法.它的名字和动态没有关系,是Richard Bellman为了唬人而取的. 动态规划 ...
- C++用递归实现斐波那契数列
[题目描述] 菲波那契数列是指这样的数列: 数列的第一个和第二个数都为1,接下来每个数都等于前面2个数之和. 给出一个正整数a,要求菲波那契数列中第a个数是多少. [输入] 第1行是测试数据的组数n, ...
- python_递归_斐波那契
什么是递归算法? -- 函数自己调用自己本身 -- 本质上return返回的时候,总是把一个参数传入到自己函数本身,让函数反复调用下去 递归有何特点? -- 必有一个结束条件 没有结束条件,递归就没有 ...
- 剑指offer编程题Java实现——面试题9斐波那契数列
题目:写一个函数,输入n,求斐波那契数列的第n项. package Solution; /** * 剑指offer面试题9:斐波那契数列 * 题目:写一个函数,输入n,求斐波那契数列的第n项. * 0 ...
随机推荐
- Android java.lang.NoSuchFieldError: No static field xxx of type I in class Lcom/XX/R$id; or its superclasses
项目开发快到尾声,突然发现之前一个模块莫名其妙的奔溃了,我的内心也是奔溃的.以前一直都是好好的,也没去动过它,为啥会出现这样的问题呢? 下面我会根据自己的理解来看待问题 android是怎么根据id查 ...
- Ajax往后台传参数,无参数,一个参数,多个参数,一个对象等
原文:http://www.cnblogs.com/chenwolong/p/Get.html //无参数请求-简单示例 $(document).ready(function () { $.ajax( ...
- C# 爬虫总结
static void Main(string[] args) { //WebRequest request = WebRequest.Create("http://www.cnblogs. ...
- WPF通用管理框架 项目客户端基础结构介绍
介绍 首先, 粗糙的展示一下目前的结构设计理念, 因为这几天一直在忙于工作, 所以跟进有些缓慢, 整体的设计是支持多种服务模式.目前只针对MSSQL做数据库接口, ORM选型则用的是微软的EF(PS: ...
- UVALive-6485-Electric Car Rally(BFS)
题目:点击打开链接 思路:对于当前位置的每个时间段都要走一遍(除了那些须要的时间比最大同意的时间还大的),用 整形 vis[当前位置][剩余油量] 标记. #include <cstdio> ...
- Monkey服务器命令
- golang round
func Round(f float64, n int) float64 {pow10_n := math.Pow10(n)return math.Trunc((f+0.5/pow10_n)*pow1 ...
- 【2017 Multi-University Training Contest - Team 7】Hard challenge
[Link]:http://acm.hdu.edu.cn/showproblem.php?pid=6127 [Description] 平面上有n个点,每个点有一个价值,每两个点之间都有一条线段,定义 ...
- 【2017"百度之星"程序设计大赛 - 初赛(B)】小小粉丝度度熊
[链接]http://acm.hdu.edu.cn/showproblem.php?pid=6119 [题意] 在这里写题意 [题解] 先把相交的部分合成一个区间. 这个可以用排序,加个简单的处理就能 ...
- 让ie6 7 8 9支持原生html5 websocket
让ie6 7 8 9支持原生html5 websocket 从github上的 web-socket-js(socket.io好像也是用这个做的他们的flash替代传输方式)改过来的.不过值得 ...
