【XSY3350】svisor - 点分治+虚树dp

题目来源：NOI2019模拟测试赛（九）

题意：

吐槽：

第一眼看到题觉得这不是震波的完全弱化版吗……然后开开心心的码了个点分治

码到一半突然发现看错题了……心态崩了于是就弃疗手玩提答去了

于是就快乐垫底了

最后发现这是个最毒瘤的题……改题写+调了一天，代码长度再次进入前五排行榜

题解：

（明明是在线做法为什么不强制在线呢）

由于是询问树上某些关键点的信息，且$\sum k$比较小，所以考虑建出虚树处理询问；

如图，对于虚树上一个不是关键点的点$u$，显然他的最大监视半径就是$max\{r_v-dis_{u,v}|v是u的子节点\}$；

这个可以通过逆拓扑序在虚树上一遍DP求出来；

由于虚树的点数是$O(k)$的，所以可以直接用点分治预处理离每个点距离小于等于$r$的点数量，然后$O(logn)$处理虚树上所有点的询问；

但是这样做显然会有点被重复计算，如图，阴影部分的点就被计算了两次（图中是一条链，实际上可能还有其它分支也被重复计算了）；

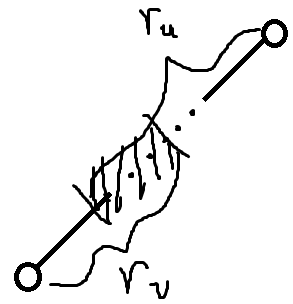
考虑被重复计算的部分有什么性质，容易发现它实际上就是距离$u$和$v$的监视半径重叠部分中心不超过$\frac{r_u+r_v-dis_{u,v}}{2}$的点集，显然这也可以当成类似的询问用点分治处理；

对虚树上每一对有重叠的父子都类似处理一遍，就可以减去所有重叠部分的额外影响，因此不用额外考虑被覆盖了三次四次甚至以上的点；

由于虚树的边数=点数-1，所以这一部分的时间复杂度显然是对的；

但是这样还有一个小问题：如图，如果重叠部分边长度为奇数，那么是找不到中心点的；

实际上这时中心点在一条边上，所以可以拆边，把树上每条原本的边都看成一个点，就可以解决了；

至此这道题终于做完了……具体实现的时候并不用把虚树真正建出来，只记录每个点的父节点和拓扑序即可；

总的时间复杂度$O((n+\sum k)logn)$，常数很大。

写的时候细节超多……外面的点分治要记一万个信息……轻松喜提200行+

代码：

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<cmath>
 #include<queue>
 #include<stack>
 #define inf 2147483647
 #define eps 1e-9
 using namespace std;
 typedef long long ll;
 typedef double db;
 struct edge{
     int v,next;
 }a[];
 int n,m,u,v,K,S,rt,mxd,ans,tot=,tim=,fkfa[],dfn[],nmd[],head[],dps[],md1[],*s1[],md2[],*s2[],ddp[],dfdep[],dfrt[][],dfds[][],k[],r[],siz[],mx[],dep[],fa[][];
 bool used[],isk[];
 stack<int>st;
 vector<int>vec;
 bool cmp(int a,int b){
     return dfn[a]<dfn[b];
 }
 void add(int u,int v){
     a[++tot].v=v;
     a[tot].next=head[u];
     head[u]=tot;
 }
 void dfs(int u,int ff,int dpt){
     dep[u]=dpt;
     dfn[u]=++tim;
     nmd[tim]=u;
     fa[u][]=ff;
     for(int i=;i<=;i++)fa[u][i]=fa[fa[u][i-]][i-];
     for(int tmp=head[u];tmp!=-;tmp=a[tmp].next){
         int v=a[tmp].v;
         if(v!=ff){
             dfs(v,u,dpt+);
         }
     }
 }
 int lca(int u,int v){
     if(dep[u]<dep[v])swap(u,v);
     int l=dep[u]-dep[v];
     for(int i=;i>=;i--){
         if((<<i)&l){
             u=fa[u][i];
         }
     }
     if(u==v)return u;
     for(int i=;i>=;i--){
         if(fa[u][i]!=fa[v][i]){
             u=fa[u][i],v=fa[v][i];
         }
     }
     return fa[u][];
 }
 int getfa(int u,int l){
     for(int i=;i>=;i--){
         if((<<i)&l){
             u=fa[u][i];
         }
     }
     return u;
 }
 void dfsrt(int u,int fa){
     siz[u]=;
     mx[u]=;
     mxd=max(mxd,ddp[u]);
     if(u<=n)dps[ddp[u]]++;
     for(int tmp=head[u];tmp!=-;tmp=a[tmp].next){
         int v=a[tmp].v;
         if(!used[v]&&v!=fa){
             dfsrt(v,u);
             siz[u]+=siz[v];
             mx[u]=max(mx[u],siz[v]);
         }
     }
     mx[u]=max(mx[u],S-siz[u]);
     if(mx[u]<mx[rt])rt=u;
 }
 void dfsdep(int u,int fa,int ls,int dpt){
     siz[u]=;
     ddp[u]=dpt;
     dfdep[u]++;
     dfrt[u][dfdep[u]]=ls;
     dfds[u][dfdep[u]]=dpt;
     mxd=max(mxd,dpt);
     if(u<=n)dps[dpt]++;
     for(int tmp=head[u];tmp!=-;tmp=a[tmp].next){
         int v=a[tmp].v;
         if(!used[v]&&v!=fa){
             dfsdep(v,u,ls,dpt+);
             siz[u]+=siz[v];
         }
     }
 }
 void divide(int u){
     used[u]=true;
     ddp[u]=mxd=;
     dfsdep(u,,u,);
     md1[u]=mxd;
     s1[u]=new int[mxd+];
     for(int i=;i<=mxd;i++){
         s1[u][i]=dps[i];
         if(i)s1[u][i]+=s1[u][i-];
         dps[i]=;
     }
     for(int tmp=head[u];tmp!=-;tmp=a[tmp].next){
         int v=a[tmp].v;
         if(!used[v]){
             mxd=rt=;
             S=siz[v];
             dfsrt(v,u);
             md2[rt]=mxd;
             s2[rt]=new int[mxd+];
             for(int i=;i<=mxd;i++){
                 s2[rt][i]=dps[i];
                 if(i)s2[rt][i]+=s2[rt][i-];
                 dps[i]=;
             }
             divide(rt);
         }
     }
 }
 void buildfaketree(){
     while(!st.empty())st.pop();
     vec.clear();
     sort(k+,k+K+,cmp);
     st.push(k[]);
     for(int i=;i<=K;i++){
         int z=lca(k[i],st.top());
         if(!isk[z])r[z]=-;
         while(!st.empty()&&dep[z]<dep[st.top()]){
             int x=st.top();
             st.pop();
             vec.push_back(x);
             if(!st.empty()&&dep[z]<dep[st.top()])fkfa[x]=st.top();
             else fkfa[x]=z;
         }
         if(st.empty()||dep[z]>dep[st.top()])st.push(z);
         if(k[i]!=z)st.push(k[i]);
     }
     while(!st.empty()){
         int x=st.top();
         st.pop();
         vec.push_back(x);
         if(!st.empty())fkfa[x]=st.top();
         else fkfa[x]=;
     }
 }
 int getci(int u,int r){
     int nw,d1,d2,ret=;
     for(int i=dfdep[u];i;i--){
         nw=dfrt[u][i];
         d1=dfds[u][i];
         d2=dfds[u][i-];
         if(d1<=r)ret+=s1[nw][min(r-d1,md1[nw])];
         if(i>&&d2<=r)ret-=s2[nw][min(r-d2,md2[nw])];
     }
     return ret;
 }
 void getans(){
     ans=;
     int u,ft,ds,mid,len=vec.size();
     for(int i=;i<len;i++){
         u=vec[i];
         r[fkfa[u]]=max(r[fkfa[u]],r[u]-dep[u]+dep[fkfa[u]]);
     }
     for(int i=len-;i>=;i--){
         u=vec[i];
         r[u]=max(r[u],r[fkfa[u]]-dep[u]+dep[fkfa[u]]);
     }
     for(int i=;i<len;i++){
         u=vec[i];
         ans+=getci(u,r[u]);
     }
     for(int i=;i<len-;i++){
         u=vec[i];
         ft=fkfa[u];
         ds=dep[u]-dep[ft];
         if(r[u]+r[ft]>=ds){
             mid=getfa(u,(r[u]-r[ft]+ds)/);
             ans-=getci(mid,r[u]-(r[u]-r[ft]+ds)/);
         }
     }
 }
 void pt(int *s){
     for(int i=;i<=n*-;i++)printf("%d ",s[i]);
     puts("");
 }
 int main(){
     memset(head,-,sizeof(head));
     scanf("%d",&n);
     for(int i=;i<n;i++){
         scanf("%d%d",&u,&v);
         add(u,n+i);
         add(n+i,u);
         add(v,n+i);
         add(n+i,v);
     }
     dfs(,,);
     S=n*-;
     mx[rt]=;
     dfsrt(,-);
     memset(dps,,sizeof(dps));
     divide(rt);
     scanf("%d",&m);
     while(m--){
         scanf("%d",&K);
         r[]=-;
         for(int i=;i<=K;i++){
             scanf("%d",&k[i]);
             scanf("%d",&r[k[i]]);
             r[k[i]]*=;
             isk[k[i]]=true;
         }
         buildfaketree();
         for(int i=;i<=K;i++)isk[k[i]]=false;
         getans();
         printf("%d\n",ans);
     }
     return ;
 }