傅里叶变换 - Fourier Transform
傅里叶级数
傅里叶在他的专著《热的解析理论》中提出,任何一个周期函数都可以表示为若干个正弦函数的和,即:
\[f(t)=a_0+\sum_{n=1}^{\infty}(a_ncos(n\omega t)+b_nsin(n\omega t))\]其中\(\omega=\dfrac{2\pi}{T}\),\(T\)为函数的周期。\(a_n/b_n\)和\(n\)分别控制了正弦波的振幅与频率。这就是傅里叶级数的三角形式。
我们还可以用复指数形式1和积分2来表示傅里叶级数:
\[ f(t)=\sum_{n=-\infty}^{\infty}F_ne^{in\omega t} \] \[ F_n=\frac{1}{T}\int_0^T f(t)e^{-in\omega t} dt \]其中\(F\)就是周期函数\(f\)的傅里叶级数(Fourier Series, FS)。
如果说\(f\)是某段信号在时域上的表现,\(F\)就是其在频域上的表现。傅里叶变换实现的就是从时域到频域的变换。
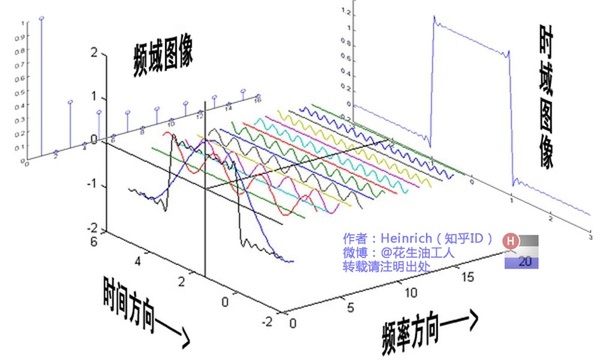
傅里叶变换
对于非周期函数,我们可以将其视为一个以\((-\infty,\infty)\)为一个周期的周期函数。
经过数学推导,得到:
\[ F(\omega)=\int_{-\infty}^\infty f(t)e^{-i\omega t} dt\] \[ f(t)=\frac{1}{2\pi}\int_{-\infty}^\infty F(\omega)e^{i\omega t} d\omega \] 这叫做傅里叶变换(Fouier Transform, FT)及傅里叶逆变换(IFT)。
注意,其结果都可能是复数。
这时,\(F\)不再是离散的级数,而是一个连续的函数了。
与傅里叶级数的比较:
- 傅里叶级数:周期信号,离散频率,频率分量的值
- 傅里叶变换:非周期信号,连续频率,频率分量的密度
卷积定理
卷积定理有两个:
\[ FT[f_1(t)*f_2(t)]=FT[f_1(t)]\cdot FT[f_2(t)] \] \[ IFT[F_1(\omega)*F_2(\omega)]=\frac{1}{2\pi}IFT[F_1(\omega)]\cdot IFT[F_2(\omega)] \] 分别称为时域卷积定理和频域卷积定理。
下面对时域卷积定理进行证明。
\[
\begin{align}
FT[f_1(t)*f_2(t)] &= FT[\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau) d\tau] \\
&= \int_{-\infty}^\infty[\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau) d\tau]e^{-i\omega t} dt \\
&= \int_{-\infty}^\infty f_1(\tau)[\int_{-\infty}^\infty f_2(t-\tau)e^{-i\omega t} dt]d\tau \\
&= \int_{-\infty}^\infty f_1(\tau)[\int_{-\infty}^\infty f_2(t)e^{-i\omega (t+\tau)} dt]d\tau \\
&= \int_{-\infty}^\infty f_1(\tau)e^{-i\omega\tau}[\int_{-\infty}^\infty f_2(t)e^{-i\omega t} dt]d\tau \\
&= \int_{-\infty}^\infty f_1(\tau)e^{-i\omega\tau}F_2(\omega) d\tau \\
&= F_2(\omega) \int_{-\infty}^\infty f_1(\tau)e^{-i\omega\tau} d\tau \\
&= F_1(\omega)F_2(\omega)
\end{align}
\] 其实基本上就是直接展开啦。频域卷积定理的证明也是类似的。
可以观察到,在一个域上进行卷积,相当于在另一个域上进行点积。这启发我们用复杂度低的点积运算来代替复杂度高的卷积运算。
离散时间傅里叶变换
以上的内容都是针对连续信息/连续函数的。但是,计算机是无法存储连续的信息的,只能每隔时间\(T\)对信息进行采样。也就是说,计算机把连续的函数转化为了离散的序列。对于这样一个序列进行的傅里叶变换就称为离散时间傅里叶变换(Discrete Time Fouier Transform, DTFT)。
\[ F(\omega)=\sum_{n=-\infty}^\infty f(nT)e^{-i\omega nT } \] 我们其实是用离散的采样点\(nT\)代替了FT中连续的时间\(t\)。进一步,由于采样的结果本质上是一个序列,那么我们可以把序列中连续两项的间隔,也就是采样频率\(T\)看做单位“1”。我们用\(x(n)\)表示采样结果序列,那么有:
\[ X(\omega)=\sum_{n=-\infty}^\infty x(n)e^{-i\omega n} \] 事实上,这个将\(T\)转化为“1”的过程,就是模拟信号转化为数字信号的过程。
其逆变换IDTFT的表达式为:
\[ x(n)=\int_{-\pi}^\pi X(\omega)e^{i\omega n} d\omega\]
离散傅里叶变换
通过DTFT,我们已经能够处理离散的采样信号了。但由于采样结果序列依然是无限长的,计算机还是无法进行处理。从DTFT的式子中可以看出,\(X(\omega)\)是以\(2\pi\)为周期的,那么解决的方法很简单:我们只从时域\((0,2\pi)\)上均匀地取\(N\)个点,用这\(N\)个点计算出频域上的\(N\)个点,这\(N\)个点就可以作为频域上的一个周期。
\[ X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk} \quad (k=0,1,2...,N-1)\] 其中\(W_N=e^{-i\frac{2\pi}{N}}\),也就是n次单位根。
其实DFT就是将DTFT中的对\(\omega\)积分替换为对\(\frac{2k\pi}{N}\)求和3。
这样,我们就得到了一个\(N\)点信号到\(N\)点频域的离散变换,这个变换就叫做离散傅里叶变换(Discrete Fourier Transform, DFT)。
其逆变换的表达式为:
\[ x(n)=\frac{1}{N} \sum_{k=0}^{N-1}X(k)W_N^{-nk} \quad (n=0,1,2...,N-1)\]
FS, FT, DTFT, DFT的比较
| 变换 | 特点 |
|- -|- -|
|傅里叶级数FS | 周期信号,离散频率,频率分量的值
|傅里叶变换FT | 非周期信号,连续频率,频率分量的密度
|离散时间傅里叶变换DTFT | 非周期采样信号,连续频率,频率分量的密度
|离散傅里叶变换DFT | 有限长度非周期采样信号,离散频率,对于DTFT频谱频率分量的密度
快速傅里叶变换
朴素进行DFT的复杂度是\(O(n^2)\),这可以从其表达式中看出。事实上我们有一种利用分治进行DFT的\(O(nlogn)\)算法,这就是常常被应用在OI中的快速傅里叶变换(Fast Fourier Transform, FFT)。
为了方便,以下若不做特殊说明,\(N\)均是\(2\)的整数次幂,这可以通过在原来的序列后补若干个\(0\)至有\(2\)的整数次幂项来实现。
\[
\begin{align}
X(k) &= \sum_{n=0}^{N-1}x(n)W_N^{nk} \\
&= \sum_{n=0,n+=2}^{N-2}x(n)W_N^{nk} + \sum_{n=1,n+=2}^{N-1}x(n)W_N^{nk} \\
&= \sum_{n=0}^{\frac{N}{2}-1}x(2n)W_N^{2nk} + \sum_{n=0}^{\frac{N}{2}-1}x(2n+1)W_N^{(2n+1)k} \\
&= \sum_{n=0}^{\frac{N}{2}-1}x(2n)W_{\frac{N}{2}}^{nk} + W_N\sum_{n=0}^{\frac{N}{2}-1}x(2n+1)W_{\frac{N}{2}}^{nk}
\end{align}
\] 通过以上变形,原问题变成了两个规模减半的子问题。合并两个子问题的复杂度是\(O(1)\),分治层数为\(O(logn)\),所以计算一项的复杂度是\(O(logn)\),计算\(n\)项的复杂度是\(O(nlogn)\)。
例题:多项式乘法
设\(n\)次多项式\(f_1(x)=\sum_{i=0}^{n}a_ix^i\)和\(m\)次多项式\(f_2(x)=\sum_{i=0}^{m}b_ix^i\)的积为\(n+m\)次多项式\(f_3(x)=\sum_{i=0}^{n+m}c_ix^i\)。给出序列\(a,b\),求序列\(c\)。
容易知道\(c_k=\sum_{i=0}^{k}a_ib_{k-i}\),事实上序列\(c\)就是序列\(a\)和序列\(b\)的离散卷积。
那么根据卷积定理,\(c_k=IDFT[DFT[c_k]]=IDFT[DFT[a_k*b_k]]=IDFT[DFT[a_k]\cdot DFT[b_k]]\)
所以我们只要将序列\(a\)和\(b\)DTFT到频域,点积后再IDTFT回时域,就可以得到序列\(c\)啦。
时间复杂度\(O((n+m)log(n+m))\)。
快速数论变换
在我们进行DTFT的过程中,使用的是复数。如果精度要求很高(比如求方案数),用复数来进行FFT就会出现误差。所以我们需要找到一个与复数单位根有相似性质的替代。
注意到FFT能够进行的根本因素就是复数单位根具有\(W_N^2=W_{\frac{N}{2}}\)这一性质。事实上,模意义域下的原根4就是复数单位根的一个很好的替代。
定义\(W_N=g^{\frac{P-1}{N}}(mod \ P)\),则有:
\[ X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk} \quad (mod \ P)\] 这就是快速数论变换(Number Theory Transform, NTT)。
进行NTT时,最常用的模数就是998244353,其原根\(g=3\)。
傅里叶变换 - Fourier Transform的更多相关文章
- 短时傅里叶变换(Short Time Fourier Transform)原理及 Python 实现
原理 短时傅里叶变换(Short Time Fourier Transform, STFT) 是一个用于语音信号处理的通用工具.它定义了一个非常有用的时间和频率分布类, 其指定了任意信号随时间和频率变 ...
- 【OI向】快速傅里叶变换(Fast Fourier Transform)
[OI向]快速傅里叶变换(Fast Fourier Transform) FFT的作用 在学习一项算法之前,我们总该关心这个算法究竟是为了干什么. (以下应用只针对OI) 一句话:求多项式 ...
- 从傅里叶级数(Fourier series)到离散傅里叶变换(Discrete Fourier transform)
从傅里叶级数(Fourier series)到离散傅里叶变换(Discrete Fourier transform) 一. 傅里叶级数(FS) 首先从最直观的开始,我们有一个信号\(x(t)\)(满足 ...
- 数字图像处理实验(5):PROJECT 04-01 [Multiple Uses],Two-Dimensional Fast Fourier Transform 标签: 图像处理MATLAB数字图像处理
实验要求: Objective: To further understand the well-known algorithm Fast Fourier Transform (FFT) and ver ...
- 「学习笔记」Fast Fourier Transform
前言 快速傅里叶变换(\(\text{Fast Fourier Transform,FFT}\) )是一种能在\(O(n \log n)\)的时间内完成多项式乘法的算法,在\(OI\)中的应用很多,是 ...
- 使用 scipy.fft 进行Fourier Transform:Python 信号处理
摘要:Fourier transform 是一个强大的概念,用于各种领域,从纯数学到音频工程甚至金融. 本文分享自华为云社区<使用 scipy.fft 进行Fourier Transform:P ...
- 【manim】3b1b的"Almost" Fourier Transform复刻
最近在做Fourier Transform的内容,记录一下今天下午的成果. 本文代码全部自行编写,需要math and music项目完整工程可以在gayhub上获取.(现在还没弄完,就先不发了.) ...
- Fast Fourier Transform ——快速傅里叶变换
问题: 已知$A=a_{0..n-1}$, $B=b_{0..n-1}$, 求$C=c_{0..2n-2}$,使: $$c_i = \sum_{j=0}^ia_jb_{i-j}$$ 定义$C$是$A$ ...
- 快速傅里叶变换(Fast Fourier Transform, FFT)和短时傅里叶变换(short-time Fourier transform,STFT )【资料整理】【自用】
1. 官方形象展示FFT:https://www.bilibili.com/video/av19141078/?spm_id_from=333.788.b_636f6d6d656e74.6 2. 讲解 ...
随机推荐
- Python--socketserve源码分析(一)
class ThreadingTCPServer(ThreadingMixIn, TCPServer): pass 实现原理: s =socketserver.ThreadingTCPServer(参 ...
- 【Shell脚本学习指南笔记】重定向文件描述符 2>&1
如: make > results 2>&1 重定向 > results让文件描述符1(标准输出)作为文件results,接下来的重定向2>&1有两个部分.2& ...
- 理解js中的作用域,作用域链以及闭包
作用域变量作用域的类型:全局变量和局部变量全局作用域对于最外层函数定义的变量拥有全局作用域,即对任何内部函数来说,都是可以访问的 <script> var outerVar = " ...
- Codeforce B. Polycarp and Letters
B. Polycarp and Letters time limit per test 2 seconds memory limit per test 256 megabytes input stan ...
- [UWP]合体姿势不对的HeaderedContentControl
1. 前言 HeaderedContentControl是WPF中就存在的控件,这个控件的功能很简单:提供Header和Content两个属性,在UI上创建两个ContentPresenter并分别绑 ...
- 填坑:在 SegmentFault 开发单页应用之图片引用的问题探索
前言 前段时间,SegmentFault 低调上线了 技术号 模块,方便用户对数据进行集中管理.在开发过程中,第一次引入了 MV* 框架. SF 的基本架构还是后端路由,这也使得页面频繁地整体请求,体 ...
- BZOJ 3993: [SDOI2015]星际战争 [二分答案 二分图]
3993: [SDOI2015]星际战争 题意:略 R1D2T1考了裸二分答案+二分图最大匹配... #include <iostream> #include <cstdio> ...
- js跨域解决方案
1.参考该文档:http://blog.csdn.net/enter89/article/details/51205752 2. 参考网络:http://www.ruanyifeng.com/blog ...
- 腾讯IVWEB前端工程化工具feflow思考与实践
本篇文章主要介绍腾讯IVWEB团队从0到1在工程化的思考和实践.feflow的全称是Front-end flow(前端工作流),致力于提升研发效率和规范的工程化解决方案.愿景是通过feflow,可以使 ...
- 炸金花的JS实现从0开始之 -------现在什么都不会(1)
新年结束了.回想起来唯一留下乐趣的就是在家和朋友玩玩炸金花. 遂有此文. 对不起,我这时候还没有思路. 让我捋一捋. ... ... 捋一捋啊... ... 好了.今天先这样吧: (1)先整理出所有的 ...
