StopAllSounds

10月3日,在杭州市西湖景区,一只小松鼠不停地接受一道道食物,花生、
玉米、饼干,可谓来者不拒,憨态可掬的模样吸引了众多围观者...
Description  
 小松鼠开心地在树之间跳跃着,突然她停了下来。因为眼前出现了一个
拿着专克超萌小松鼠的法宝————超萌游戏机的游客!
 超萌游戏机之所以拥有这个名字,是因为它的屏幕是一个n × 2的矩形。
小松鼠接过游戏机,开始了她的第一个游戏:俄罗斯方块。
 考虑到小松鼠的智商,游戏机里的方块只有下面四种,方块按顺序下落,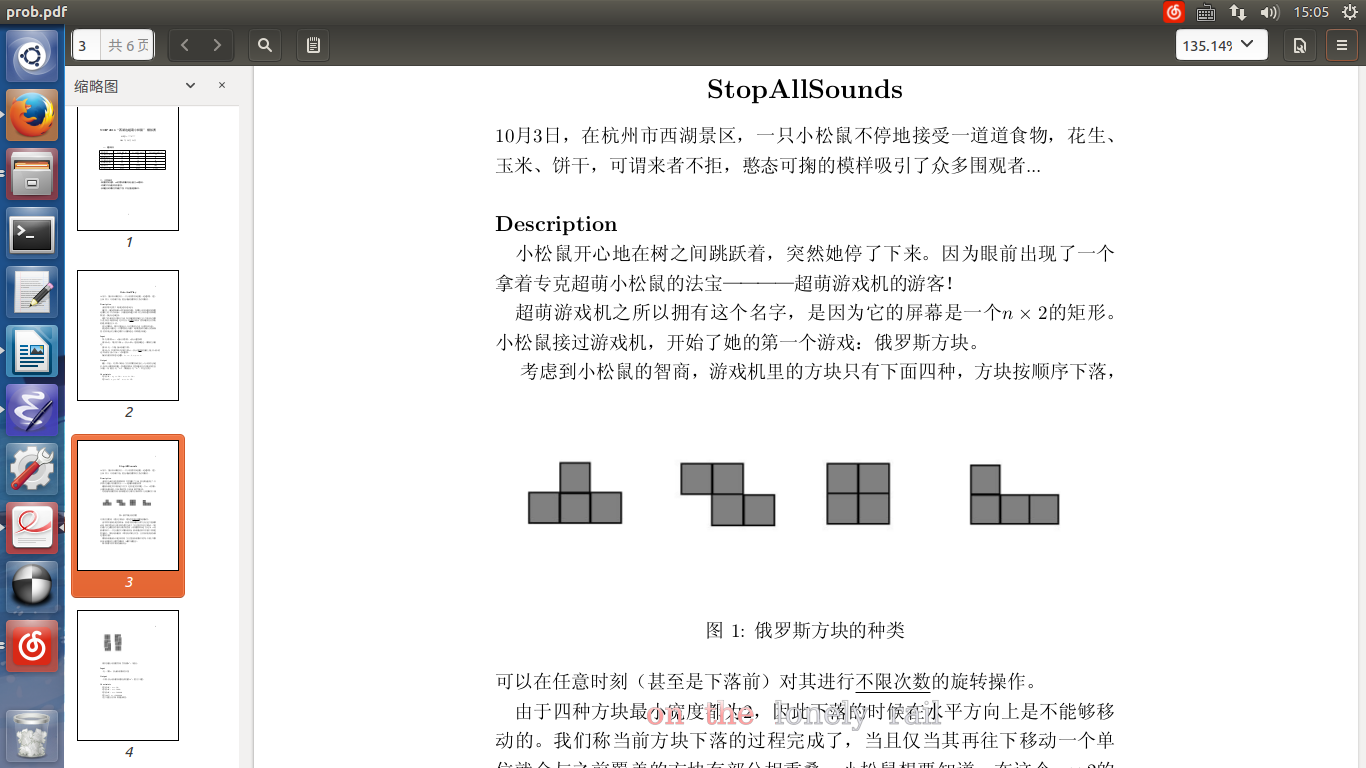

（Linux太垃圾了，不带画图）
可以在任意时刻(甚至是下落前)对其进行不限次数的旋转操作。
 由于四种方块最小宽度都为2,因此下落的时候在水平方向上是不能够移
动的。我们称当前方块下落的过程完成了,当且仅当其再往下移动一个单
位就会与之前覆盖的方块有部分相重叠。小松鼠想要知道,在这个n × 2的
游戏界面中,一共会出现多少种游戏状态。游戏状态指单次方块下落的过
程完成后,不要求游戏结束(即不要求第1行非空),且界面中出现的必须
是完整的方块。

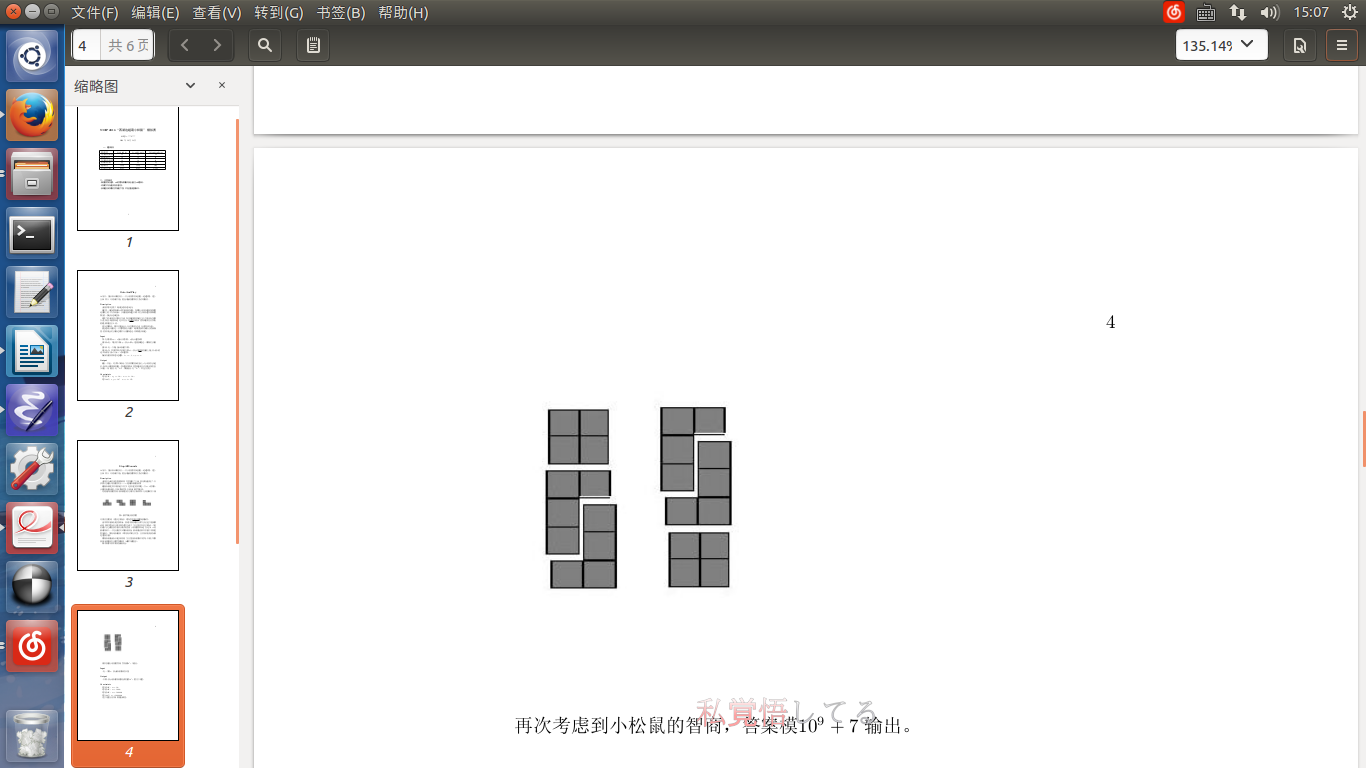
 两种游戏状态被认为是相同的,当且仅当游戏界面中的每一个格子两种
状态下被覆盖的方块类型都相同(或都不被覆盖) 。
 如下图属于两种不同的游戏状态
 再次考虑到小松鼠的智商,答案模10 9 + 7 输出。
Input  
 一行一个数n,表示游戏界面的长度。
Output  
 一个数,表示游戏界面的状态数在模10 9 + 7意义下的值。
Constraints  
 对于前10%,n <= 10。
 对于前30%,n <= 1000。
 对于前60%,n <= 100000。
 对于100%,n <= 1000000。
 人生不能失去信仰,数据有梯度。

f[i][0]表示第i行2列都满了

f[i][1]表示第i行第1列为空

f[i][2]表示第i行第2列为空

f[i][3]表示第i,i-1行第一列都为空

f[i][4]表示第i,i-1行第二列都为空

f[i][5]表示第i行为空

记住：方块只能旋转，未填满也算方案

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 using namespace std;
 long long f[][];
 int n;
 int Mod=;
 int main()
 {int i,j;
   cin>>n;
   f[][]=;
   for (i=;i<=n;i++)
     {
       if (i>=)
     f[i][]+=f[i-][]+f[i-][]+f[i-][]+f[i-][]+f[i-][];
       f[i][]%=Mod;
       if (i>=)
     f[i][]+=f[i-][]+f[i-][]+f[i-][]+f[i-][]+f[i-][],
       f[i][]+=f[i-][]+f[i-][]+f[i-][]+f[i-][]+f[i-][];
       f[i][]%=Mod;
       f[i][]%=Mod;
       if (i>=)
     f[i][]+=f[i-][]+f[i-][]+f[i-][]+f[i-][]+f[i-][];
        // f[i][2]+=f[i-2][2]+f[i-2][4]+f[i-3][0]+f[i-3][1]+f[i-3][3];
       f[i][]%=Mod;f[i][]%=Mod;
       if (i>=)
     f[i][]+=f[i-][]+f[i-][]+f[i-][]+f[i-][]+f[i-][],
       //f[i][4]+=f[i-3][0]+f[i-3][1]+f[i-3][2]+f[i-3][3]+f[i-3][4],
       f[i][]+=f[i-][]+f[i-][]+f[i-][]+f[i-][]+f[i-][];
       f[i][]=f[i-][]+f[i-][]+f[i-][]+f[i-][]+f[i-][]+f[i-][];
       f[i][]%=Mod;f[i][]%=Mod;f[i][]%=Mod;f[i][]%=Mod;
     }
   //cout<<f[4][5]<<endl;
   //printf("%d %d %d %d %d\n",f[n][5],f[n][4],f[n][3],f[n][2],f[n][1],f[n][0]);
   cout<<((f[n][]+f[n][])%Mod+(f[n][]+f[n][])%Mod+(f[n][]+f[n][])%Mod)%Mod;
 }