http://blog.csdn.net/pipisorry/article/details/51461997

最大似然估计MLE

顾名思义，当然是要找到一个参数，使得L最大，为什么要使得它最大呢，因为X都发生了，即基于一个参数发生的，那么当然就得使得它发生的概率最大。

最大似然估计就是要用似然函数取到最大值时的参数值作为估计值，似然函数可以写做

Note: p(x|theta)不总是代表条件概率；也就是说p(x|theta)不代表条件概率时与p(x;theta)等价，而一般地写竖杠表示条件概率，是随机变量；写分号p(x; theta)表示待估参数（是固定的，只是当前未知）,应该可以直接认为是p(x)，加了;是为了说明这里有个theta的参数，p(x; theta)意思是随机变量X=x的概率。在贝叶斯理论下又叫X=x的先验概率。相乘因为它们之间是独立同分布的。由于有连乘运算，通常对似然函数取对数计算简便，即对数似然函数。

最大似然估计问题可以写成

这是一个关于的函数，求解这个优化问题通常对求导，得到导数为0的极值点。该函数取得最大值是对应的的取值就是我们估计的模型参数。

给定观测到的样本数据，一个新的值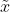发生的概率是

求出参数值不是最终目的，最终目的是去预测新事件基于这个参数下发生的概率。

Note: 注意有一个约等于，因为他进行了一个近似的替换，将theta替换成了估计的值，便于计算。that is, the next sample is anticipated to be distributed with the estimated parameters θ ˆ ML .

扔硬币的伯努利实验示例

以扔硬币的伯努利实验为例子，N次实验的结果服从二项分布，参数为P，即每次实验事件发生的概率，不妨设为是得到正面的概率。为了估计P，采用最大似然估计，似然函数可以写作

其中表示实验结果为i的次数。下面求似然函数的极值点，有

得到参数p的最大似然估计值为

可以看出二项分布中每次事件发的概率p就等于做N次独立重复随机试验中事件发生的概率。

如果我们做20次实验，出现正面12次，反面8次，那么根据最大似然估计得到参数值p为12/20 = 0.6。

[Gregor Heinrich: Parameter estimation for text analysis*]

MLE的一个最简单清晰的示例

皮皮blog

最大似然估计MLE

能最大化已观测到的观测序列的似然的参数就是估计的参数值。

图钉的例子

为不同参数theta的可能值打分并选择的一种标准

一般情况下的MLE

最大似然准则

参数模型和参数空间

似然函数的定义

充分统计量

MLE的注解

MLE的缺陷：置信区间

似然函数度量了参数选择对于训练数据的影响。

似然函数的要求

[《Probabilistic Graphical Models：Principles and Techniques》(简称PGM)]

皮皮blog
from: http://blog.csdn.net/pipisorry/article/details/51461997

ref:

参数估计：最大似然估计MLE的更多相关文章

  1. 极大似然估计MLE 极大后验概率估计MAP

    https://www.cnblogs.com/sylvanas2012/p/5058065.html 写的贼好 http://www.cnblogs.com/washa/p/3222109.html ...

  2. 【MLE】最大似然估计Maximum Likelihood Estimation

    模型已定,参数未知 已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值.最大似然估计是建立在这样的思想上:已知某个参数能使这个 ...

  3. 【ML数学知识】极大似然估计

    它是建立在极大似然原理的基础上的一个统计方法,极大似然原理的直观想法是,一个随机试验如有若干个可能的结果A,B,C,... ,若在一次试验中,结果A出现了,那么可以认为实验条件对A的出现有利,也即出现 ...

  4. ML 徒手系列 最大似然估计

    1.最大似然估计数学定义: 假设总体分布为f(x,θ),X1,X2...Xn为总体采样得到的样本.其中X1,X2...Xn独立同分布,可求得样本的联合概率密度函数为: 其中θ是需要求得的未知量,xi是 ...

  5. 又看了一次EM 算法，还有高斯混合模型，最大似然估计

    先列明材料: 高斯混合模型的推导计算(英文版): http://www.seanborman.com/publications/EM_algorithm.pdf 这位翻译写成中文版: http://w ...

  6. B-概率论-极大似然估计

    [TOC] 更新.更全的<机器学习>的更新网站,更有python.go.数据结构与算法.爬虫.人工智能教学等着你:https://www.cnblogs.com/nickchen121/ ...

  7. LR为什么用极大似然估计，损失函数为什么是log损失函数（交叉熵）

    首先,逻辑回归是一个概率模型,不管x取什么值,最后模型的输出也是固定在(0,1)之间,这样就可以代表x取某个值时y是1的概率 这里边的参数就是θ,我们估计参数的时候常用的就是极大似然估计,为什么呢?可 ...

  8. Maximum Likelihood 最大似然估计

    Maximum Likelihood 最大似然估计 这个算法解决的问题是,当我们知道一组变量的密度分布函数与从总体采样的个体的时候,需要估计函数中的某些变量. 假设概率密度函数如下: 一般来说,为了计 ...

  9. 似然估计中为什么要取对数以GMM为例

    1.往往假设特征之间独立同分布,那么似然函数往往是连城形式,直接求骗到不好搞,根据log可以把连乘变为连加. 2.另外概率值是小数,多个小数相乘容易赵成浮点数下溢,去log变为连加可以避免这个问题. ...

随机推荐

  1. bzoj2237[NCPC2009]Flight Planning 结论题？

    2237: [NCPC2009]Flight Planning Time Limit: 10 Sec  Memory Limit: 256 MBSubmit: 55  Solved: 27[Submi ...

  2. bzoj2811[Apio2012]Guard 贪心

    2811: [Apio2012]Guard Time Limit: 10 Sec  Memory Limit: 128 MBSubmit: 905  Solved: 387[Submit][Statu ...

  3. [APIO/ctsc2007]

    A.风铃 给一棵二叉树,叶子结点是玩具,为使你的弟弟满意,你需要选一个满足下面两个条件的风铃: (1) 所有的玩具都在同一层(也就是说,每个玩具到天花板之间的杆的个数是一样的)或至多相差一层.(2) ...

  4. MySQL插件实现浅析——插件的调用

    一. MySQL中的动态插件 最初想到这个问题是在学习mysql半同步复制相关问题的时候,为何在mysql运行时install半同步插件并开启后就能起到作用,他是如何让事务停下来等待的.安装插件的时候 ...

  5. super 关键字

  6. Java8——快速入门手册（学习笔记）

    github博文传送门 Java8特性学习笔记 Java8中新增了许多的新特性,在这里本人研究学习了几个较为常用的特性,在这里与大家进行分享.(这里推荐深入理解Java 8用于理解基础知识)本文分为以 ...

  7. js改变dom对象样式

    object.style.display = value; objcet对象必须是确定单个对象. 若以class名和标签名查找,需要指定对象集合中的第几个.

  8. 47. Permutations II(medium, backtrack, 重要, 条件较难思考)

    Given a collection of numbers that might contain duplicates, return all possible unique permutations ...

  9. DOS/Windows 文本格式与 Unix 文本各式转换

    命令简介: dos2unix是将Windows格式文件转换为Unix.Linux格式的实用命令.Windows格式文件的换行符为\r\n ,而Unix&Linux文件的换行符为\n. dos2 ...

  10. python 常用镜像

    pip镜像https://pypi.tuna.tsinghua.edu.cn/simplehttps://pypi.douban.io.com/simple pip install python-qt ...