数据集偏斜 - class skew problem - 以SVM松弛变量为例

原文

接下来要说的东西其实不是松弛变量本身，但由于是为了使用松弛变量才引入的，因此放在这里也算合适，那就是惩罚因子C。回头看一眼引入了松弛变量以后的优化问题：

注意其中C的位置，也可以回想一下C所起的作用（表征你有多么重视离群点，C越大越重视，越不想丢掉它们）。这个式子是以前做SVM的人写的，大家也就这么用，但没有任何规定说必须对所有的松弛变量都使用同一个惩罚因子，我们完全可以给每一个离群点都使用不同的C，这时就意味着你对每个样本的重视程度都不一样，有些样本丢了也就丢了，错了也就错了，这些就给一个比较小的C；而有些样本很重要，决不能分类错误（比如中央下达的文件啥的，笑），就给一个很大的C。

当然实际使用的时候并没有这么极端，但一种很常用的变形可以用来解决分类问题中样本的“偏斜”问题。

先来说说样本的偏斜问题，也叫数据集偏斜（unbalanced），它指的是参与分类的两个类别（也可以指多个类别）样本数量差异很大。比如说正类有10，000个样本，而负类只给了100个，这会引起的问题显而易见，可以看看下面的图：

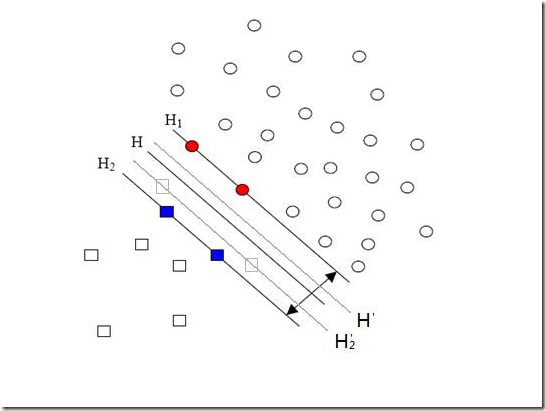
方形的点是负类。H，H₁，H₂是根据给的样本算出来的分类面，由于负类的样本很少很少，所以有一些本来是负类的样本点没有提供，比如图中两个灰色的方形点，如果这两个点有提供的话，那算出来的分类面应该是H’，H₂’和H₁，他们显然和之前的结果有出入，实际上负类给的样本点越多，就越容易出现在灰色点附近的点，我们算出的结果也就越接近于真实的分类面。但现在由于偏斜的现象存在，使得数量多的正类可以把分类面向负类的方向“推”，因而影响了结果的准确性。

对付数据集偏斜问题的方法之一就是在惩罚因子上作文章，想必大家也猜到了，那就是给样本数量少的负类更大的惩罚因子，表示我们重视这部分样本（本来数量就少，再抛弃一些，那人家负类还活不活了），因此我们的目标函数中因松弛变量而损失的部分就变成了：

其中i=1…p都是正样本，j=p+1…p+q都是负样本。libSVM这个算法包在解决偏斜问题的时候用的就是这种方法。

那C₊和C_-怎么确定呢？它们的大小是试出来的（参数调优），但是他们的比例可以有些方法来确定。咱们先假定说C₊是5这么大，那确定C_-的一个很直观的方法就是使用两类样本数的比来算，对应到刚才举的例子，C_-就可以定为500这么大（因为10，000：100=100：1嘛）。

但是这样并不够好，回看刚才的图，你会发现正类之所以可以“欺负”负类，其实并不是因为负类样本少，真实的原因是负类的样本分布的不够广（没扩充到负类本应该有的区域）。说一个具体点的例子，现在想给政治类和体育类的文章做分类，政治类文章很多，而体育类只提供了几篇关于篮球的文章，这时分类会明显偏向于政治类，如果要给体育类文章增加样本，但增加的样本仍然全都是关于篮球的（也就是说，没有足球，排球，赛车，游泳等等），那结果会怎样呢？虽然体育类文章在数量上可以达到与政治类一样多，但过于集中了，结果仍会偏向于政治类！所以给C₊和C_-确定比例更好的方法应该是衡量他们分布的程度。比如可以算算他们在空间中占据了多大的体积，例如给负类找一个超球——就是高维空间里的球啦——它可以包含所有负类的样本，再给正类找一个，比比两个球的半径，就可以大致确定分布的情况。显然半径大的分布就比较广，就给小一点的惩罚因子。

但是这样还不够好，因为有的类别样本确实很集中，这不是提供的样本数量多少的问题，这是类别本身的特征（就是某些话题涉及的面很窄，例如计算机类的文章就明显不如文化类的文章那么“天马行空”），这个时候即便超球的半径差异很大，也不应该赋予两个类别不同的惩罚因子。

看到这里读者一定疯了，因为说来说去，这岂不成了一个解决不了的问题？然而事实如此，完全的方法是没有的，根据需要，选择实现简单又合用的就好（例如libSVM就直接使用样本数量的比）。