机器学习——KMeans聚类，KMeans原理，参数详解

0.聚类

　　聚类就是对大量的未知标注的数据集，按数据的内在相似性将数据集划分为多个类别，使类别内的数据相似度较大而类别间的数据相似度较小，聚类属于无监督的学习方法。

1.内在相似性的度量

　　聚类是根据数据的内在的相似性进行的，那么我们应该怎么定义数据的内在的相似性呢？比较常见的方法是根据数据的相似度或者距离来定义的，比较常见的有：

• 闵可夫斯基距离/欧式距离

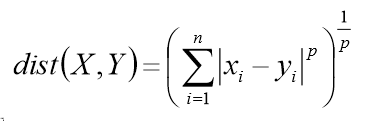
　　上述距离公式中，当p=2时，就是欧式距离，当p=1时，就是绝对值的和，当p=正无穷时，这个距离变成了维度差最大的那个值。

• 杰卡德相似系数

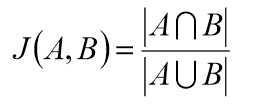
　　一般是度量集合之间的相似性。

• 余弦相似度

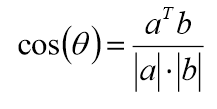
• Pearson相似系数

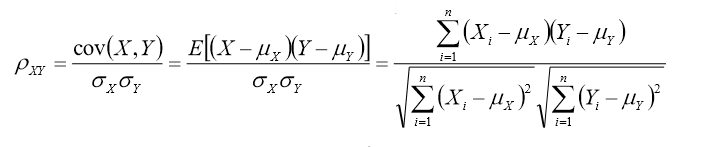
　　对于n维向量的夹角，根据余弦定理，可到：

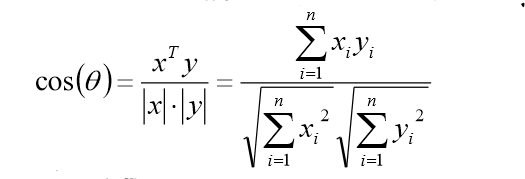
　　又由相关系数的计算公式，可得：

　　不难发现，相关系数就是将x，y坐标向量各自平移到原点后的夹角余弦。

• 相对熵（K-L距离）

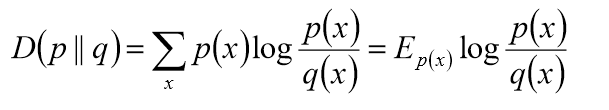
2.聚类的基本思想

　　1.给定一个有N个对象的数据集，构造数据的K个簇，k<=n，并且满足下列条件：

　　　　每一个簇至少包含一个对象。

　　　　每一个对象属于且仅属于一个簇。

　　　　将满足上述条件的K个簇称作一个合理划分。

　　2.基本思想：对于给定的类别K，首先给定初始的划分，通过迭代改变样本和簇的隶属关系，使得每一次改进之后的划分方案都较前一次好。

3.K-Means算法

　　K-means算法，也被称为K-平均或K-均值，是一种广泛使用的聚类算法，或者成为其他聚类算法的基础。

　　假定输入样本为S=x1, x2, ......, xm，则算法步骤为：

　　　　选择初始的k个类别中心，u1, u2, ......, uk。

　　　　对于每个样本的xi，将其中标记为距离类别中心最近的类别，即：

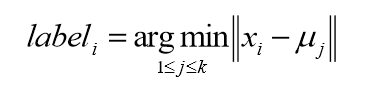
　　将每个类别中心更新为隶属该类别的所有样本的均值。

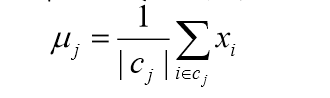
　　重复后面的两步，直到类别中心变化小于某阈值。

　　终止条件：

　　　　迭代次数，簇中心变化率，最小平方误差MSE。

4.K-Means的公式化解释

　　记K个簇中心为u1,u2,......,uk，每个簇的样本数目为N1,N2,......，Nk。

　　使用平方误差作为目标函数：

　　该函数为关于u1,u2,......,uk的凸函数，计算其驻点，得：

5.K-Means聚类方法总结

优点：

　　一种经典算法，简单，快速的聚类算法。

　　对于大数据集，该算法保持可伸缩性和高效率。

　　当簇近似为高斯分布时，它的效果较好。

缺点：

　　在簇的平均值可被定义的情况下才能使用，可能不适用某些情况。

　　必须实现给出K(聚类的簇数目)，而且是初值敏感的，对于不同的初始值，可能会导致不同的结果。

　　不适合于发现非凸型的簇或者大小差别很大的簇。

　　对噪声和孤立点数据敏感。

　　在很多情况下，可以作为其他聚类的基础算法，比如谱聚类。

6.代码示例

 if __name__ == '__main__':
     N = 400
     centers = 4
     data1, y1 = make_blobs(n_samples=N, n_features=2, centers= centers, random_state=2)
     data2, y2 = make_blobs(n_samples=N, n_features=2, centers=centers, cluster_std=(1, 2.5, 0.5, 2), random_state=2)
     plt.figure()
     plt.plot(data1[:, 0], data1[:, 1], 'ro', data2[:, 0], data2[:, 1], 'g*')
     plt.show()
 
     data = np.vstack((data1[y1 == 0][:], data1[y1 == 1][:50], data1[y1 == 2][:20], data1[y1 == 3][:5]))
     y = np.array([0] * 100 + [1] * 50 + [2] * 20 + [3] * 5)
     # print(data)
     # print(y)
     # plt.figure()
     # plt.plot(data[:100, 0], data[:100, 1], 'ro',
     #          data[100:150, 0], data[100:150, 1], 'g*',
     #          data[150:170, 0], data[150:170, 1], 'b*',
     #          data[170:175, 0], data[170:175, 1], 'k*')
     # plt.show()
 
     cls = KMeans(n_clusters=4, init='k-means++')
     y1_hat = cls.fit_predict(data1)
     y2_hat = cls.fit_predict(data2)
     y_hat = cls.fit_predict(data)
     # print(y1_hat)

KMeans函数的参数详解：

　　n_clusters：整型，缺省值=8 ，生成的聚类数。
　　max_iter：整型，缺省值=300 。
　　　　执行一次k-means算法所进行的最大迭代数。
　　n_init：整型，缺省值=10 。
　　　　　 用不同的聚类中心初始化值运行算法的次数，最终解是在inertia意义下选出的最优结果。
　　init：有三个可选值：’k-means++’， ‘random’，或者传递一个ndarray向量。
　　　　 此参数指定初始化方法，默认值为 ‘k-means++’。
　　　　（１）‘k-means++’ 用一种特殊的方法选定初始聚类中发，可加速迭代过程的收敛。
　　　　（２）‘random’ 随机从训练数据中选取初始质心。
　　　　（３）如果传递的是一个ndarray，则应该形如 (n_clusters, n_features) 并给出初始质心。
　　precompute_distances：三个可选值，‘auto’，True 或者 False。
　　　　预计算距离，计算速度更快但占用更多内存。
　　　　（１）‘auto’：如果 样本数乘以聚类数大于 12million 的话则不预计算距离。
　　　　（２）True：总是预先计算距离。
　　　　（３）False：永远不预先计算距离。
　　tol：float类型，默认值= 1e-4　与inertia结合来确定收敛条件。
　　n_jobs：整形数。　指定计算所用的进程数。内部原理是同时进行n_init指定次数的计算。
　　　　（１）若值为 -1，则用所有的CPU进行运算。若值为1，则不进行并行运算。
　　　　（２）若值小于-1，则用到的CPU数为(n_cpus + 1 + n_jobs)。因此如果 n_jobs值为-2，则用到的CPU数为总CPU数减1。
　　random_state：整型或 numpy.RandomState 类型，可选
　　　　　用于初始化质心的生成器（generator）。如果值为一个整数，则确定一个seed。此参数默认值为numpy的随机数生成器。
　　copy_x：布尔型，默认值=True 　　
　　　　　　 当我们precomputing distances时，将数据中心化会得到更准确的结果。如果把此参数值设为True，则原始数据不会被改变。如果是False，则会直接在原始数据
　　　　　　上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算，所以数据返回后，原始数据和计算前可能会有细小差别。
聚类结果：

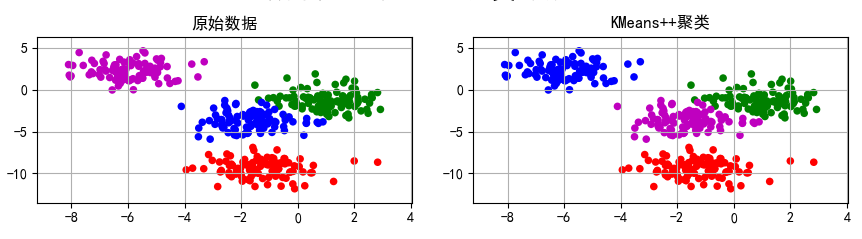
在聚类的过程中，我们发现，如果对数据进行一定的变化，得到的聚类结果可能有所不同，比如旋转。