高斯消元（Gauss消元）

众所周知，高斯消元可以用来求n元一次方程组的，主要思想就是把一个n*(n+1)的矩阵的对角线消成1，除了第n+1列（用来存放b的）的其他全部元素消成0，是不是听起来有点不可思议？？！

NO NO NO！

这不就是初中学的代入消元和加减消元嘛，思路一样的。

Step 1：将所给出的n元1次方程组的每个未知数系数和等号后面的常数写成一个n*(n+1)的矩阵

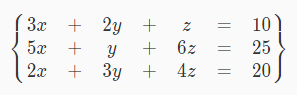
比如这个三元一次方程组我们就可以写成如下3×4的矩阵：

Step 2 ：运用矩阵的各种性质，来将矩阵消成对角线上的元素为1，并且除了第n+1列其余元素均为0的矩阵，

这样我们就很容易的得出每个未知数的值：分别是从上到下第n+1列的值（因为这时候每个未知数的系数都为1）

那么是神马神奇性质呐？？？找度娘啊

（1） 任意交换矩阵的两行或两列，矩阵不变；

（2）矩阵任意行或列ai加上或减去任意k倍的任意行或列（ai行也可以加减k倍的ai行），矩阵不变；

………………………………

其余的性质这里就用不到啦，这两条性质足矣。

好啦，下面说一下怎么个消法（重点 嘤嘤嘤～）

以上面的矩阵为例：

明确我们的目的：把矩阵消成对角线为1，除了第n+1列其余元素都为0

也就是说，每一列都至少有一个元素不为0，若有一列全为0肯定有第i行第i列消不成1，此时无解

不理解的话也可以从方程组的数学角度来思考一下：

我们把每个未知数的系数写成矩阵，所以矩阵的某一列就是某一未知数的全部系数，

如果全为0，那么不就是没有这个未知数吗？那么这个未知数的值就不能确定了，那不就是无解吗？对吧。

知道了这个，我们就可以对这个矩阵进行初步判定：

for(int i=;i<=n;i++)
    {
        pl=i;                      //从第i行开始往下找，一直找到一个第i列不为0的行
        while(a[pl][i]==&&pl<=n)
        pl++;
         // 判断第i列元素非0的最上行，因为第i行第i列元素不能为0
        if(pl==n+) {cout<<"No Solution";return ;}
        //一直判到了n+1行，可是一共才只有n行，说明有一列全为0，无解
                 for(int j=;j<=n+;j++)
                //将第i行元素与第pl行第i列不为0的那一行与当前行交换
        swap(a[i][j],a[pl][j]);   //保证第i行第i列不为0
        }

这样一来，我们就保证了第i行第i列的元素不为0，可是我们要让第i行第i列的值整成1啊，我们可以用性质（2），让第i行的每个元素都除以第i行第i列的值

注意：这里用到了除法，就有可能出现小数，所以我们要用double类型定义二维数组矩阵

        double k=a[i][i];                          //让第i行每个元素都除以a[i][i]使得a[i][i]为1
        for(int j=;j<=n+;j++)
        a[i][j]=a[i][j]/k;                         //将第i行第i列的元素消成1,注意同行进行同样的操作

我们就让第i行第i列的元素搞成1列，继续完成接下来的任务：顺便把第i列的其他元素搞成0；

我们已经把第i行的搞成了1，所以我们只要把其余行的每个元素都减去本行的首元素*第i行的对应元素（为什么是第i行呢？仗着第i行第i列的元素是1比较好消）

        for(int j=;j<=n;j++)
        {
            if(i!=j)                        //将第i列除了第i行的元素全消成0
            {                               //方法是第j行每个元素a[j][m]都减去a[j][1]*a[i][m]
                double ki=a[j][i];
                for(int m=;m<=n+;m++)
                a[j][m]=a[j][m]-ki*a[i][m];
            }
        }
    

到这里就OK啦，最后输出第n+1列的元素就是每个未知数的解啦!

完整代码如下：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int n,pl;
double a[][];
int main()
{
    cin>>n;
    for(int i=;i<=n;i++)
       for(int j=;j<=n+;j++)
       cin>>a[i][j];
    for(int i=;i<=n;i++)
    {
        pl=i;
        while(a[pl][i]==&&pl<=n)
        pl++;
         // 判断第i列首元素非0的最上行，因为第i行第i列元素不能为0
        if(pl==n+) {cout<<"No Solution";return ;}
        //一直判到了n+1行，可是一共才只有n行，说明有一列全为0，无解
        for(int j=;j<=n+;j++)             //将第i行第i列元素不为0的那一行与当前行交换
        swap(a[i][j],a[pl][j]);
        double k=a[i][i];                          //让第i行每个元素都除以a[i][i]使得a[i][i]为1
        for(int j=;j<=n+;j++)
        a[i][j]=a[i][j]/k;                         //将第i行第i列的元素消成1,注意同行进行同样的操作
        for(int j=;j<=n;j++)
        {
            if(i!=j)                        //将第i列除了第i行的元素全消成0
            {                               //方法是第j行每个元素a[j][m]都减去a[j][1]*a[i][m]
                double ki=a[j][i];
                for(int m=;m<=n+;m++)
                a[j][m]=a[j][m]-ki*a[i][m];
            }
        }
    }
    for(int i=;i<=n;i++)
    printf("%.2lf\n",a[i][n+]);
    return ;
}

QWQ，大家一定跃跃欲试了吧，给大家推荐一个洛谷板子题，巩固一下吧。

【模板】高斯消元法